
【题目】如图,AD是∠BAC平分线,点E在AB上,且AE=AC,EF∥BC交AC于点F,AD与CE交于点G,与EF交于点H.
(1)证明:AD垂直平分CE;
(2)若∠BCE=40°,求∠EHD的度数.

【答案】(1)见解析;(2)50°.
【解析】
(1)根据等腰三角形三线合一的性质可得出结论;(2)由(1)可知点D为CE垂直平分线上的点,则CD=DE,∠DCE=∠DEC.由EF∥BC,可得EG平分∠DEF;由EG⊥AD,可证∠EDH=∠EHD,根据内角和定理,即可得出结论.
解:(1)∵AE=AC,AD是∠BAC平分线,
∴AD垂直平分CE;
(2)由(1)可知点D为CE垂直平分线上的点,
∴CD=DE,
∴∠DCE=∠DEC.
∵EF∥BC,
∴∠DCE=∠CEF=∠DEC,
∴EG平分∠DEF.
∵EG⊥AD,EG=EG,
∴△DEG≌△HEG(ASA),
∴△DEH是等腰三角形,且ED=EH,
∴∠EDH=∠EHD,
∵∠BCE=40°,
∴∠DEH=2∠BCE=80°,
∴∠EHD=![]() (180°﹣80°)=50°.
(180°﹣80°)=50°.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】为了解某校学生的身高情况,随机抽取该校男生、女生进行抽样调查.已知抽取的样本中,男生、女生的人数相同,利用所得数据绘制如下统计图表: 身高情况分组表(单位:cm)
组别 | 身高 |
A | x<155 |
B | 155≤x<160 |
C | 160≤x<165 |
D | 165≤x<170 |
E | x≥170 |
根据图表提供的信息,回答下列问题:
(1)样本中,男生的身高众数在组,中位数在组;
(2)样本中,女生身高在E组的人数有人;
(3)已知该校共有男生400人,女生380人,请估计身高在160≤x<170之间的学生约有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一辆货车从仓库O出发在东西街道上运送水果,规定向东为正方向,一次到达的5个销售地点依次分别为A,B,C,D,E,最后回到仓库O,货车行驶的记录(单位:千米)如下:+1,+3,﹣6,﹣1,﹣2,+5.请问:
(1)请以仓库O为原点,向东为正方向,选择适当的单位长度,画出数轴,并标出A,B,C,D,E的位置;
(2)试求出该货车共行驶了多少千米?
(3)如果货车运送的水果以100千克为标准重量,超过的千克数记为正数,不足的千克数记为负数,则运往A,B,C,D,E五个地点的水果重量可记为:
+50,﹣15,+25,﹣10,﹣15,则该货车运送的水果总重量是多少千克?
查看答案和解析>>
科目:初中数学 来源: 题型:
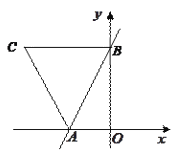
【题目】如图,已知一次函数![]() 的图像与x轴、
的图像与x轴、![]() 轴分别交于点A、B,且BC∥AO,梯形AOBC的面积为10.
轴分别交于点A、B,且BC∥AO,梯形AOBC的面积为10.
(1)求点A、B、C的坐标;
(2)求直线AC的表达式.
查看答案和解析>>
科目:初中数学 来源: 题型:
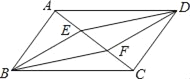
【题目】如图,在□ABCD中,E,F是对角线AC上的两点且AE=CF,在①BE=DF;②BE∥DF;③AB=DE;④四边形EBFD为平行四边形;⑤S△ADE=S△ABE;⑥AF=CE这些结论中正确的是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,AB⊥BC,AD∥BC,∠BCD=120°,BC=2,AD=DC.P为四边形ABCD边上的任意一点,当∠BPC=30°时,CP的长为 . 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,PA、PB分别与⊙O相切于点A、B,点M在PB上,且OM∥AP,MN⊥AP,垂足为N. 
(1)求证:OM=AN;
(2)若⊙O的半径R=3,PA=9,求OM的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,AB=15,BC=14,AC=13,求△ABC的面积.
某学习小组经过合作交流,给出了下面的解题思路,请你按照他们的解题思路完成解答过程.
思路:(1) 作AD⊥BC于D,设BD = x,用含x的代数式表示CD;(2)根据勾股定理,利用AD作为“桥梁”,建立方程模型,求出x;(3)利用勾股定理求出AD的长,再计算三角形面积.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com