
分析 结合图形两腰长的差就是腰长与底边的差,因为腰长与底边的大小不明确,所以分腰长大于底边和腰长小于底边两种情况讨论.
解答 解:根据题意,分成两部分的周长的差等于腰长与底边的差,
(1)若AB>BC,则AB-BC=4,
又因为2AB+BC=16,
联立方程组得:$\left\{\begin{array}{l}{AB-BC=4}\\{2AB+BC=16}\end{array}\right.$,
解得:AB=$\frac{20}{3}$,BC=$\frac{8}{3}$,
$\frac{20}{3}$cm、$\frac{20}{3}$cm、$\frac{8}{3}$cm三边能够组成三角形;
(2)若AB<BC,则BC-AB=4,
又因为2AB+BC=16,
联立方程组得:$\left\{\begin{array}{l}{BC-AB=4}\\{2AB+BC=16}\end{array}\right.$,
解得:AB=4,BC=8,
4cm、4cm、8cm三边不能够组成三角形;
因此三角形的各边长为$\frac{20}{3}$cm、$\frac{20}{3}$cm、$\frac{8}{3}$cm.
点评 本题主要考查等腰三角形的性质及三角形三边关系;做题中利用了分类讨论的思想,注意运用三角形三边关系对三角形的组成情况作出判断,这是解题的关键.


 鹰派教辅衔接教材河北教育出版社系列答案
鹰派教辅衔接教材河北教育出版社系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
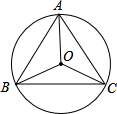 如图是一个旋转对称图形,以O为旋转中心,以下列哪一个角为旋转角旋转,能使旋转后的图形与原图形重合( )
如图是一个旋转对称图形,以O为旋转中心,以下列哪一个角为旋转角旋转,能使旋转后的图形与原图形重合( )| A. | 60° | B. | 150° | C. | 180° | D. | 240° |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com