
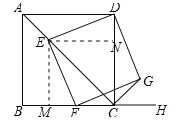
【题目】如图,已知四边形ABCD为正方形,AB=![]() ,点E为对角线AC上一动点,连接DE,过点E作EF⊥DE.交射线BC于点F,以DE、EF为邻边作矩形DEFG,连接CG.
,点E为对角线AC上一动点,连接DE,过点E作EF⊥DE.交射线BC于点F,以DE、EF为邻边作矩形DEFG,连接CG.
①求证:矩形DEFG是正方形;
②探究:CE+CG的值是否为定值?若是,请求出这个定值;若不是,请说明理由.

【答案】(1)见解析;(2) 是定值
【解析】分析:①作出辅助线,得到EN=EM,然后判断∠DEN=∠FEM,得到△DEN≌△FEM,则有DE=EF即可;
②同①的方法证出△ADE≌△CDG得到CG=AE,得出CE+CG=CE+AE=AC=4即可.
详解:①过E作EM⊥BC于M点,过E作EN⊥CD于N点,如图所示:
∵正方形ABCD,
∴∠BCD=90°,∠ECN=45°,
∴∠EMC=∠ENC=∠BCD=90°, 且NE=NC,∴四边形EMCN为正方形.
∵四边形DEFG是矩形,∴EM=EN,∠DEN+∠NEF=∠MEF+∠NEF=90°,
∴∠DEN=∠MEF,又∠DNE=∠FME=90°.在△DEN和△FEM中,∵∠DNE=∠FME,EN=EM,∠DEN=∠FEM,∴△DEN≌△FEM(ASA),∴ED=EF,∴矩形DEFG为正方形,
②CE+CG的值为定值,理由如下:
∵矩形DEFG为正方形,∴DE=DG,∠EDC+∠CDG=90°.
∵四边形ABCD是正方形,∵AD=DC,∠ADE+∠EDC=90°,
∴∠ADE=∠CDG.在△ADE和△CDG中,∵AD=CD,∠ADE=∠CDG,DE=DG,∴△ADE≌△CDG(SAS),∴AE=CG,
∴AC=AE+CE=![]() AB=
AB=![]() ×2
×2![]() =4,∴CE+CG=4 是定值.
=4,∴CE+CG=4 是定值.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】将从1开始的连续自然数按图规律排列:规定位于第m行,第n列的自然数10记为(3,2),自然数15记为(4,2)…
列 行 | 第1列 | 第2列 | 第3列 | 第4列 |
第1行 | 1 | 2 | 3 | 4 |
第2行 | 8 | 7 | 6 | 5 |
第3行 | 9 | 10 | 11 | 12 |
第4行 | 16 | 15 | 14 | 13 |
… | … | … | … | … |
第n行 | … | … | … | … |
按此规律,回答下列问题:
(1)记为(6,3)表示的自然数是__________________.
(2)自然数2018记为_________________.
(3)用一个正方形方框在第span>3列和第4列中任意框四个数,这四个数的和能为2018吗?如果能,求出框出的四个数中最小的数;如果不能,请写出理由。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线AB与⊙O相切于点A,AC、CD是⊙O的两条弦,且CD∥AB,若⊙O的半径为 ![]() ,CD=4,则弦AC的长为( )
,CD=4,则弦AC的长为( ) 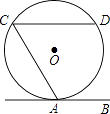
A.2 ![]()
B.3 ![]()
C.4
D.2 ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】同学们都知道:|5|在数轴上表示数5的点与原点的距离,而|5-(-2)|表示5与-2之差的绝对值,实际上也可理解为5与-2两数在数轴上所对应的两点之间的距离.请你借助数轴进行以下探索:
![]()
(1)则![]() 表示 的距离.
表示 的距离.
(2)数轴上表示x与 7的两点之间的距离可以表示为 .
(3)如果|x-2|=5,则x= .
(4)同理|x+1|+|x-2|表示数轴上有理数x所对应的点到-1和2所对应的点的距离之和,请你找出所有符合条件的整数x,使得|x+1|+|x-2|=3,这样的整数是 .
(5)由以上探索猜想对于任何有理数x,|x+3|+|x-6|的最小值是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在有些情况下,不需要计算出结果也能把绝对值符号去掉.例如:
|6+7|= 6+7 ;|6-7|=7-6;|7-6|=7- 6;|-6-7|=6+7;
(1)根据上面的规律,把下列各式写成去掉绝对值符号的形式:
①|7-21|= ;
②![]() = ;
= ;
(2)数a在数轴上的位置如图所示,则|a-2.5|=( )
A.a-2.5 B.2.5-a C.a+2.5 D.-a-2.5
![]()
(3)用合理的方法计算:![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD是平行四边形,点E在边BC上,如果点F是边AD上的点,那么△CDF与△ABE不一定全等的条件是( )
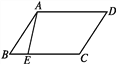
A. DF=BE B. AF=CE
C. CF=AE D. CF∥AE
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:△ABC在直角坐标平面内,三个顶点的坐标分别为A(0,3)、B(3,4)、C(2,2)(正方形网格中每个小正方形的边长是一个单位长度).
(1)画出△ABC向下平移4个单位长度得到的△A1B1C1 , 点C1的坐标是;
(2)以点B为位似中心,在网格内画出△A2B2C2 , 使△A2B2C2与△ABC位似,且位似比为2:1,点C2的坐标是;
(3)△A2B2C2的面积是平方单位.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,AB=AC,AD是△ABC的角平分线,点O为AB的中点,连接DO并延长到点E,使OE=OD,连接AE,BE.
(1)求证:四边形AEBD是矩形;
(2)当△ABC满足什么条件时,矩形AEBD是正方形?并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,ABCD中,E,F是对角线BD上的两点,如果添加一个条件,使△ABE≌△CDF,则添加的条件不能为( )

A. BE=DF B. BF=DE C. AE=CF D. ∠1=∠2
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com