
【题目】如图,分别以Rt△ABC的斜边AB、直角边AC为边向外作等边△ABD和△ACE,F为AB中点,连接DF、EF,DE、EF与AC交于点O,DE与AB交于点G,连接OG,若∠BAC=30°,下列结论:①△DBF≌△EFA;②AD=AE;③EF⊥AC;④AD=4AG;⑤△AOG与△EOG的面积比为1:4.其中正确的结论的序号是_____.

【答案】①③④
【解析】
根据等边三角形的性质求出∠EAC=60°,AE=AC,求出BC=AF,根据SAS证△ABC≌△EFA,推出FE=AB,∠AEF=∠BAC=30°,求出∠AOE=90°,即可判断③;求出AD=BD,BF=AF,∠DFB=∠EAF,∠BDF=∠AEF,根据AAS证△DBF≌△EFA,即可判断①;得出四边形ADFE为平行四边形,推出AG=![]() AF,AG=
AF,AG=![]() AB,求出AD=AB,推出AD=4AG,即可判断④;求出∠FAE=90°,∠AFE<90°,推出EF>AE,即可判断②;根据平行四边形性质得出AG=GF,推出S三角形AGOS三角形GOF,设AG=1,则AF=2,AB=4,BC=2,由勾股定理求出AC=2
AB,求出AD=AB,推出AD=4AG,即可判断④;求出∠FAE=90°,∠AFE<90°,推出EF>AE,即可判断②;根据平行四边形性质得出AG=GF,推出S三角形AGOS三角形GOF,设AG=1,则AF=2,AB=4,BC=2,由勾股定理求出AC=2![]() ,求出AO=OC,由勾股定理求出OE=3,得出△GOF和△EGO的面积比是1:3,即可判断⑤.
,求出AO=OC,由勾股定理求出OE=3,得出△GOF和△EGO的面积比是1:3,即可判断⑤.
解:∵△ACE是等边三角形,
∴∠EAC=60°,AE=AC,
∵∠BAC=30°,
∴∠FAE=∠ACB=90°,AB=2BC,
∵F为AB的中点,
∴AB=2AF,
∴BC=AF,
在△ABC和△EFA中
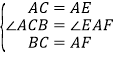 ,
,
∴△ABC≌△EFA(SAS),
∴FE=AB,∠AEF=∠BAC=30°,
∠AOE=180°-30°-60°=90°,
∴EF⊥AC,∴③正确,
∵AD=BD,BF=AF,
∴∠DFB=90°,∠BDF=30°,
∵∠FAE=∠BAC+∠CAE=90°,
∴∠DFB=∠EAF,
∵EF⊥AC,
∴∠AEF=30°,
∴∠BDF=∠AEF,
在△DBF和△EFA中
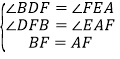 ,
,
∴△DBF≌△EFA(AAS),∴①正确;
∴AE=DF,
∵FE=AB,
∴四边形ADFE为平行四边形,
∴AG=![]() AF,AG=
AF,AG=![]() AB,
AB,
∵AD=AB,
则AD=4AG,∴④正确;
∵四边形ADFE为平行四边形,
∴AD=EF,
∵∠FAE=90°,∠AFE<90°,
∴EF>AE,
即AD>AE,∴②错误;
∵四边形ADFE为平行四边形,
∴AG=GF,
∴S三角形AGO=S三角形GOF,
设AG=1,则AF=2,AB=4,BC=2,由勾股定理得:AC=2![]() ,
,
∠CAE=60°,∠AEF=∠CAB=30°,
∴∠COE=30°+60°=90°=∠AOE,
∵AE=CE,
∴AO=OC,
在等边三角形ACE中,AE=AC=2![]() ,AO=OC=
,AO=OC=![]() ,
,
由勾股定理得:OE=![]() =3,
=3,
∵△GOF的边OF和△EGO的边OE上的高相等,
∴△GOF和△EGO的面积比是1:3,
即△AOG与△EOG的面积比为1:3,∴⑤错误;
正确的有①③④,
故答案为:①③④.


科目:初中数学 来源: 题型:
【题目】随着中国传统节日“端午节”的临近,东方红商场决定开展“欢度端午,回馈顾客”的让利促销活动,对部分品牌粽子进行打折销售,其中甲品牌粽子打八折,乙品牌粽子打七五折,已知打折前,买6盒甲品牌粽子和3盒乙品牌粽子需660元;打折后,买50盒甲品牌粽子和40盒乙品牌粽子需要5200元.
(1)打折前甲、乙两种品牌粽子每盒分别为多少元?
(2)阳光敬老院需购买甲品牌粽子80盒,乙品牌粽子100盒,问打折后购买这批粽子比不打折节省了多少钱?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有关部门从甲、乙两个城市所有的自动售货机中分别随机抽取了16台,记录下某一天各自的销售情况(单位:元):
甲:18,8,10,43,5,30,10,22,6,27,25,58,14,18,30,41
乙:22,31,32,42,20,27,48,23,38,43,12,34,18,10,34,23
小强用如图所示的方法表示甲城市16台自动售货机的销售情况.
(1)请你仿照小强的方法将乙城市16台自动售货机的销售情况表示出来;
(2)请你观察图1,你能从图1中获取哪些信息?(至少写出两条不同类型信息)
(3)小芳用图2的条形统计图表示甲城市16台自动售货机的销售情况,请你观察图2,你能从图2中获取哪些信息?(至少写出两条不同类型信息)
(4)如果收集到的数据很多,例如有200个,你认为图1和图2这两种统计图用哪一种更能直观的反映这些数据分布的大致情况?请说明理由.


查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=BC,以AB为直径的⊙O交BC于点D,交AC于点F,过点C作CE∥AB,与过点A的切线相交于点E,连接AD.
(1)求证:AD=AE;
(2)若AB=6,AC=4,求AE的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,直线l:y=![]() x+m与x轴、y轴分别交于点A和点B(0,﹣1),抛物线y=
x+m与x轴、y轴分别交于点A和点B(0,﹣1),抛物线y=![]() x2+bx+c经过点B,与直线l的另一个交点为C(4,n).
x2+bx+c经过点B,与直线l的另一个交点为C(4,n).
(1)求n的值和抛物线的解析式;
(2)点D在抛物线上,DE∥y轴交直线l于点E,点F在直线l上,且四边形DFEG为矩形(如图2),设点D的横坐标为t(0<t<4),矩形DFEG的周长为p,求p与t的函数关系式以及p的最大值;
(3)将△AOB绕平面内某点M旋转90°或180°,得到△A1O1B1,点A、O、B的对应点分别是点A1、O1、B1.若△A1O1B1的两个顶点恰好落在抛物线上,那么我们就称这样的点为“落点”,请直接写出“落点”的个数和旋转180°时点A1的横坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】箱子里有3个红球和2个黄球,从箱子中一次拿两个球出来.
(1)请你用列举法(树形图或列表)求一次拿出的两个球中时一红一黄的概率;
(2)往箱子中再加入x个白球,从箱子里一次拿出的两个球,多次实验统计如下
取出两个球的次数 | 20 | 30 | 50 | 100 | 150 | 200 | 400 |
至少有一个球是白球的次数 | 13 | 20 | 35 | 71 | 107 | 146 | 288 |
至少有一个球是白球的频率 | 0.65 | 0.67 | 0.70 | 0.71 | 0.713 | 0.73 | 0.72 |
请你估计至少有一个球是白球的概率是多少?
(3)在(2)的条件下求x的值.(![]() =0.7222222…)
=0.7222222…)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,直线l:y=![]() x+m与x轴、y轴分别交于点A和点B(0,﹣1),抛物线y=
x+m与x轴、y轴分别交于点A和点B(0,﹣1),抛物线y=![]() x2+bx+c经过点B,与直线l的另一个交点为C(4,n).
x2+bx+c经过点B,与直线l的另一个交点为C(4,n).
(1)求n的值和抛物线的解析式;
(2)点D在抛物线上,DE∥y轴交直线l于点E,点F在直线l上,且四边形DFEG为矩形(如图2),设点D的横坐标为t(0<t<4),矩形DFEG的周长为p,求p与t的函数关系式以及p的最大值;
(3)将△AOB绕平面内某点M旋转90°或180°,得到△A1O1B1,点A、O、B的对应点分别是点A1、O1、B1.若△A1O1B1的两个顶点恰好落在抛物线上,那么我们就称这样的点为“落点”,请直接写出“落点”的个数和旋转180°时点A1的横坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在 Rt△ABC 中,∠ACB=90°,BC=5,点 P 在边 AB 上,连接 CP.将△BCP 沿直线CP 翻折后,点 B 恰好落在边 AC 的中点处,则点 P 到 AC 的距离是( )

A. 2.5 B. ![]() C. 3.5 D.
C. 3.5 D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】王强同学用10块高度都是2cm的相同长方体小木块,垒了两堵与地面垂直的木墙,木墙之间刚好可以放进一个等腰直角三角板(AC=BC,∠ACB=90°),点C在DE上,点A和B分别与木墙的顶端重合,则两堵木墙之间的距离为______cm.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com