
【题目】如图,在△ABC中,AB=BC,以AB为直径的⊙O交BC于点D,交AC于点F,过点C作CE∥AB,与过点A的切线相交于点E,连接AD.
(1)求证:AD=AE;
(2)若AB=6,AC=4,求AE的长.

【答案】(1)详见解析;(2)![]() .
.
【解析】
(1)利用平行线的性质,圆的性质和等腰三角形的性质,证明△AEC和△ADC全等即可证明AD=AE,
(2)设AE=AD=x,CE=CD=y,利用勾股定理列出关于x和y的等式,即可求出AE的长.
(1)证明:∵AE与⊙O相切,AB是⊙O的直径,
∴∠BAE=90°,∠ADB=90°,
∵CE∥AB,
∴∠E=90°,
∴∠E=∠ADB,
∵在△ABC中,AB=BC,
∴∠BAC=∠BCA,
∵∠BAC+∠EAC=90°,∠ACE+∠EAC=90°,
∴∠BAC=∠ACE,
∴∠BCA=∠ACE,
又∵AC=AC,
∴△ADC≌△AEC(AAS),
∴AD=AE;
(2)解:设AE=AD=x,CE=CD=y,
则BD=(6﹣y),
∵△AEC和△ADB为直角三角形,
∴AE2+CE2=AC2,AD2+BD2=AB2,
AB=6,AC=4,AE=AD=x,CE=CD=y,BD=(6﹣y)代入,
解得:x=![]() ,y=
,y=![]() ,
,
即AE的长为![]() .
.


 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案科目:初中数学 来源: 题型:
【题目】(阅读材料)
因式分解:![]() .
.
解:将“![]() ”看成整体,令
”看成整体,令![]() ,则原式
,则原式![]() .
.
再将“![]() ”还原,原式
”还原,原式![]() .
.
上述解题用到的是“整体思想”,整体思想是数学解题中常用的一种思想方法.
(问题解决)
(1)因式分解:![]() ;
;
(2)因式分解:![]() ;
;
(3)证明:若![]() 为正整数,则代数式
为正整数,则代数式![]() 的值一定是某个整数的平方.
的值一定是某个整数的平方.
查看答案和解析>>
科目:初中数学 来源: 题型:
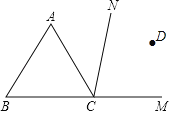
【题目】如图,CN是等边△ABC的外角∠ACM内部的一条射线,点A关于CN的对称点为D,连接AD,BD,CD,其中AD,BD分别交射线CN于点E,P.
(Ⅰ)依题意补全图形.
(Ⅱ)若∠ACN=α,求∠BDC的大小(用含α的式子表示).
(Ⅲ)若PA=x,PC=y,求PB的长度(用x,y的代数式表示).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在等腰Rt△ABC中,∠BAC=90°,点E在AC上(且不与点A、C重合).在△ABC的外部作等腰Rt△CED,使∠CED=90°,连接AD,分别以AB,AD为邻边作平行四边形ABFD,连接AF.
(1)求证:△AEF是等腰直角三角形;
(2)如图2,将△CED绕点C逆时针旋转,当点E在线段BC上时,连接AE,求证:AF=![]() AE;
AE;
(3)如图3,将△CED绕点C继续逆时针旋转,当平行四边形ABFD为菱形,且△CED在△ABC的下方时,若AB=2![]() ,CE=2,求线段AE的长.
,CE=2,求线段AE的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】把图中阴影部分的小正方形移动一个,使它与其余四个阴影部分的正方形组成一个既是轴对称又是中心对称的新图形,这样的移法,正确的是( )

A. 6→3 B. 7→16 C. 7→8 D. 6→15
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对于一次函数![]() (k,b为常数),下表中给出5组自变量及其对应的函数值:
(k,b为常数),下表中给出5组自变量及其对应的函数值:
| …… | -1 | 0 | 1 | 2 | 3 | |
| …… | -2 | 1 | 4 | 8 | 10 | …… |
其中只有1个函数值计算有误,则这个错误的函数值是( )
A.1B.4C.8D.10
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,分别以Rt△ABC的斜边AB、直角边AC为边向外作等边△ABD和△ACE,F为AB中点,连接DF、EF,DE、EF与AC交于点O,DE与AB交于点G,连接OG,若∠BAC=30°,下列结论:①△DBF≌△EFA;②AD=AE;③EF⊥AC;④AD=4AG;⑤△AOG与△EOG的面积比为1:4.其中正确的结论的序号是_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我市某中学有一块四边形的空地ABCD,如图所示,为了绿化环境,学校计划在空地上种植草皮,经测量∠A=90°,AB=3m,DA=4m,BC=12m,CD=13m.
(1)求出空地ABCD的面积.
(2)若每种植1平方米草皮需要200元,问总共需投入多少元?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,完成下列推理过程:
如图所示,点E在△ABC外部,点D在BC边上,DE交AC于F,若∠1=∠3,∠E=∠C,AE=AC,求证:△ABC≌△ADE.

证明:∵ ∠E=∠C(已知),
∠AFE=∠DFC(_________________),
∴∠2=∠3(______________________),
又∵∠1=∠3(_________________),
∴ ∠1=∠2(等量代换),
∴__________+∠DAC= __________+∠DAC(______________________),
即∠BAC =∠DAE,
在△ABC和△ADE中
∵ 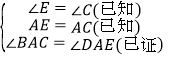
∴△ABC≌△ADE(_________________).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com