
【题目】如图,完成下列推理过程:
如图所示,点E在△ABC外部,点D在BC边上,DE交AC于F,若∠1=∠3,∠E=∠C,AE=AC,求证:△ABC≌△ADE.

证明:∵ ∠E=∠C(已知),
∠AFE=∠DFC(_________________),
∴∠2=∠3(______________________),
又∵∠1=∠3(_________________),
∴ ∠1=∠2(等量代换),
∴__________+∠DAC= __________+∠DAC(______________________),
即∠BAC =∠DAE,
在△ABC和△ADE中
∵ 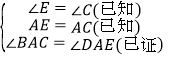
∴△ABC≌△ADE(_________________).
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=BC,以AB为直径的⊙O交BC于点D,交AC于点F,过点C作CE∥AB,与过点A的切线相交于点E,连接AD.
(1)求证:AD=AE;
(2)若AB=6,AC=4,求AE的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在 Rt△ABC 中,∠ACB=90°,BC=5,点 P 在边 AB 上,连接 CP.将△BCP 沿直线CP 翻折后,点 B 恰好落在边 AC 的中点处,则点 P 到 AC 的距离是( )

A. 2.5 B. ![]() C. 3.5 D.
C. 3.5 D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ACB=90°,CD是斜边AB上的中线,分别过点A,C作AE∥DC,CE∥AB,两线交于点E.
(1)求证:四边形AECD是菱形;
(2)如果∠B=60°,BC=2,求四边形AECD的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,直线l:y=![]() x+m与x轴、y轴分别交于点A和点B(0,﹣1),抛物线y=
x+m与x轴、y轴分别交于点A和点B(0,﹣1),抛物线y=![]() x2+bx+c经过点B,与直线l的另一个交点为C(4,n).
x2+bx+c经过点B,与直线l的另一个交点为C(4,n).
(1)求n的值和抛物线的解析式;
(2)点D在抛物线上,DE∥y轴交直线l于点E,点F在直线l上,且四边形DFEG为矩形(如图2),设点D的横坐标为t(0<t<4),矩形DFEG的周长为p,求p与t的函数关系式以及p的最大值;
(3)将△AOB绕平面内某点M旋转90°或180°,得到△A1O1B1,点A、O、B的对应点分别是点A1、O1、B1.若△A1O1B1的两个顶点恰好落在抛物线上,那么我们就称这样的点为“落点”,请直接写出“落点”的个数和旋转180°时点A1的横坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
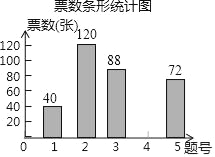
【题目】为提高三亚市初级中学教师业务水平,相关单位举办了首届“三亚市敏特杯数学命题大赛”,在众多自命题题目中共有5道题目进入专家组评审,将前5天的投票数据整理成如下不完整的统计图表:
票数条形统计图
题目编号 | 人数 | 百分比 |
1 | 40 | 10% |
2 | 120 | m% |
3 | 88 | 22% |
4 | a | 20% |
5 | 72 | 18% |
合计 | 400 | 1 |
请根据图表提供的信息,解答下面问题:
(1)票数统计表中的a= ,m= .
(2)请把票数统计图补充完整;
(3)若绘制“票数扇形统计图”编号是“4”的题目所对应扇形的圆心角是 度;
(4)至本次投票结束,总票数共有1200票,请估计编号是“3”的题目约获得 票.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】王强同学用10块高度都是2cm的相同长方体小木块,垒了两堵与地面垂直的木墙,木墙之间刚好可以放进一个等腰直角三角板(AC=BC,∠ACB=90°),点C在DE上,点A和B分别与木墙的顶端重合,则两堵木墙之间的距离为______cm.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,∠AOB内一点P,P1,P2分别P是关于OA、OB的对称点,P1P2交OA于M,交OB于N,若P1P2=6cm,则△PMN的周长是( )

A.3cmB.4cmC.5cmD.6cm
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知点A D C F在同一直线上,AB=DE,AD=CF,添加下列条件后,仍不能判断△ABC≌△DEF的是 ( )

A. BC=EFB. ∠A=∠EDFC. AB∥DED. ∠BCA=∠F
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com