
【题目】为提高三亚市初级中学教师业务水平,相关单位举办了首届“三亚市敏特杯数学命题大赛”,在众多自命题题目中共有5道题目进入专家组评审,将前5天的投票数据整理成如下不完整的统计图表:
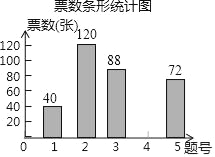
票数条形统计图
题目编号 | 人数 | 百分比 |
1 | 40 | 10% |
2 | 120 | m% |
3 | 88 | 22% |
4 | a | 20% |
5 | 72 | 18% |
合计 | 400 | 1 |
请根据图表提供的信息,解答下面问题:
(1)票数统计表中的a= ,m= .
(2)请把票数统计图补充完整;
(3)若绘制“票数扇形统计图”编号是“4”的题目所对应扇形的圆心角是 度;
(4)至本次投票结束,总票数共有1200票,请估计编号是“3”的题目约获得 票.
 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案科目:初中数学 来源: 题型:
【题目】对于一次函数![]() (k,b为常数),下表中给出5组自变量及其对应的函数值:
(k,b为常数),下表中给出5组自变量及其对应的函数值:
| …… | -1 | 0 | 1 | 2 | 3 | |
| …… | -2 | 1 | 4 | 8 | 10 | …… |
其中只有1个函数值计算有误,则这个错误的函数值是( )
A.1B.4C.8D.10
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,![]() 的顶点坐标分别为A(2,3)、B (1,1)、C(2,1)
的顶点坐标分别为A(2,3)、B (1,1)、C(2,1)

(1)画出![]() 关于
关于![]() 轴对称的
轴对称的![]() ,并写出点
,并写出点![]() 的坐标为_________
的坐标为_________
(2)将![]() 向左平移4个单位长度得到
向左平移4个单位长度得到![]() ,直接写出点
,直接写出点![]() 的坐标为_________
的坐标为_________
(3)直接写出点B关于直线n(直线n上各点的纵坐标都为-1)对称点B'的坐标为________
(4)在![]() 轴上找一点P,使PA+PB的值最小,标出P点的位置(保留画图痕迹)
轴上找一点P,使PA+PB的值最小,标出P点的位置(保留画图痕迹)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,如图,等腰Rt△ABC,等腰Rt△ADE,AB⊥AC,AD⊥AE,AB=AC,AD=AE,CD交AE、BE分别于点M、F.

(1)求证:△DAC≌△EAB.
(2)求证:CD⊥BE.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,完成下列推理过程:
如图所示,点E在△ABC外部,点D在BC边上,DE交AC于F,若∠1=∠3,∠E=∠C,AE=AC,求证:△ABC≌△ADE.

证明:∵ ∠E=∠C(已知),
∠AFE=∠DFC(_________________),
∴∠2=∠3(______________________),
又∵∠1=∠3(_________________),
∴ ∠1=∠2(等量代换),
∴__________+∠DAC= __________+∠DAC(______________________),
即∠BAC =∠DAE,
在△ABC和△ADE中
∵ 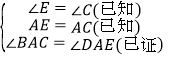
∴△ABC≌△ADE(_________________).
查看答案和解析>>
科目:初中数学 来源: 题型:
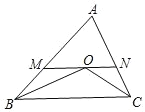
【题目】如图,在△ABC 中,∠ABC、∠ACB 的角平分线交于点 O,MN 过点 O,且MN∥BC,分别交 AB、AC 于点 M、N.若 MN=5cm,CN=2cm,则 BM=________cm.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点C、E分别在直线AB、DF上,小华想知道∠ACE和∠DEC是否互补,但是他没有带量角器,只带了一副三角板,于是他想了这样一个办法:首先连结CF,再找出CF的中点O,然后连结EO并延长EO和直线AB相交于点B,经过测量,他发现EO=BO,因此他得出结论:∠ACE和∠DEC互补,而且他还发现BC=EF.小华的想法对吗?为什么?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我国古代数学的许多创新和发展都位居世界前列,如南宋数学家杨辉所著的《详解九章算术》一书中,用如图的三角形解释二项式(a+b)n的展开式的各项系数,此三角形称为“杨辉三角”.

根据“杨辉三角”请计算(a+b)10的展开式中第三项的系数为( )
A. 2018 B. 2017 C. 55 D. 45
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下列材料,完成任务:
自相似图形
定义:若某个图形可分割为若干个都与它相似的图形,则称这个图形是自相似图形.例如:正方形ABCD中,点E、F、G、H分别是AB、BC、CD、DA边的中点,连接EG,HF交于点O,易知分割成的四个四边形AEOH、EBFO、OFCG、HOGD均为正方形,且与原正方形相似,故正方形是自相似图形.
任务:
(1)图1中正方形ABCD分割成的四个小正方形中,每个正方形与原正方形的相似比为 ;
(2)如图2,已知△ABC中,∠ACB=90°,AC=4,BC=3,小明发现△ABC也是“自相似图形”,他的思路是:过点C作CD⊥AB于点D,则CD将△ABC分割成2个与它自己相似的小直角三角形.已知△ACD∽△ABC,则△ACD与△ABC的相似比为 ;
(3)现有一个矩形ABCD是自相似图形,其中长AD=a,宽AB=b(a>b).
请从下列A、B两题中任选一条作答:我选择 题.
A:①如图3﹣1,若将矩形ABCD纵向分割成两个全等矩形,且与原矩形都相似,则a= (用含b的式子表示);
②如图3﹣2若将矩形ABCD纵向分割成n个全等矩形,且与原矩形都相似,则a= (用含n,b的式子表示);
B:①如图4﹣1,若将矩形ABCD先纵向分割出2个全等矩形,再将剩余的部分横向分割成3个全等矩形,且分割得到的矩形与原矩形都相似,则a= (用含b的式子表示);
②如图4﹣2,若将矩形ABCD先纵向分割出m个全等矩形,再将剩余的部分横向分割成n个全等矩形,且分割得到的矩形与原矩形都相似,则a= (用含m,n,b的式子表示).

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com