练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】已知：如图，∠AOB内一点P，P1，P2分别P是关于OA、OB的对称点，P1P2交OA于M，交OB于N，若P1P2＝6cm，则△PMN的周长是（　　）

    A.3cmB.4cmC.5cmD.6cm

    【答案】D

    【解析】

    由P与P1关于OA对称，得到OA为线段PP1的垂直平分线，根据线段垂直平分线的性质：线段垂直平分线上的点到线段两端点的距离相等可得MP＝MP1，同理可得NP＝NP2，由P1P2＝P1M＋MN＋NP2＝6cm，等量代换可求得△PMN的周长

    解：∵P与P1关于OA对称，

    ∴OA为线段PP1的垂直平分线，

    ∴MP＝MP1，

    同理，P与P2关于OB对称，

    ∴OB为线段PP2的垂直平分线，

    ∴NP＝NP2，

    ∴P1P2＝P1M＋MN＋NP2＝MP＋MN＋NP＝6cm，

    ∴△PMN的周长为6cm．

    故选：D．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】我市某中学有一块四边形的空地ABCD，如图所示，为了绿化环境，学校计划在空地上种植草皮，经测量∠A=90°，AB=3m，DA=4m，BC=12m，CD=13m．

    （1）求出空地ABCD的面积．

    （2）若每种植1平方米草皮需要200元，问总共需投入多少元？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，完成下列推理过程：

    如图所示，点E在△ABC外部，点D在BC边上，DE交AC于F，若∠1＝∠3，∠E＝∠C，AE＝AC，求证：△ABC≌△ADE.

    证明：∵ ∠E＝∠C（已知），

    ∠AFE＝∠DFC（_________________）,

    ∴∠2=∠3（______________________）,

    又∵∠1＝∠3（_________________）,

    ∴ ∠1=∠2（等量代换），

    ∴__________+∠DAC= __________+∠DAC（______________________）,

    即∠BAC =∠DAE,

    在△ABC和△ADE中

    ∵

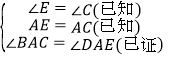
    ∴△ABC≌△ADE（_________________）.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，点C、E分别在直线AB、DF上，小华想知道∠ACE和∠DEC是否互补，但是他没有带量角器，只带了一副三角板，于是他想了这样一个办法：首先连结CF，再找出CF的中点O，然后连结EO并延长EO和直线AB相交于点B，经过测量，他发现EO＝BO，因此他得出结论：∠ACE和∠DEC互补，而且他还发现BC＝EF.小华的想法对吗？为什么？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】在学校开展的数学活动课上，小明和小刚制作了一个正三楼锥（质量均匀，四个面完全相同），并在各个面上分别标记数字1，2，3，4，游戏规则如下每人投掷三棱锥两次，并记录底面的数字，如果两次所掷数字的和为单数，那么算小明赢，如果两欢所掷数字的和为偶数，那么算小明赢；

    （1）请用列表或者面树状围的方法表示上述游戏中的所有可能结果．

    （2）请分别隶出小明和小刚能赢的概率，并判新游戏的公平性．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】我国古代数学的许多创新和发展都位居世界前列，如南宋数学家杨辉所著的《详解九章算术》一书中，用如图的三角形解释二项式（a+b）n的展开式的各项系数，此三角形称为“杨辉三角”．

    根据“杨辉三角”请计算（a+b）10的展开式中第三项的系数为（　　）

    A. 2018 B. 2017 C. 55 D. 45

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】（阅读理解）

    课外兴趣小组活动时，老师提出了如下问题：

    如图1，△ABC中，若AB＝8，AC＝6，求BC边上的中线AD的取值范围.小明在组内经过合作交流，得到了如下的解决方法：延长AD到点E，使DE＝AD，请根据小明的方法思考：

    (1)由已知和作图能得到△ADC≌△EDB的理由是_____.

    A.SSS B.SAS C.AAS D.HL

    (2)求得AD的取值范围是______.

    A.6＜AD＜8 B.6≤AD≤8 C.1＜AD＜7 D.1≤AD≤7

    （感悟）

    解题时，条件中若出现“中点”“中线”字样，可以考虑延长中线构造全等三角形，把分散的已知条件和所求证的结论集合到同一个三角形中.

    （问题解决）

    (3)如图2，AD是△ABC的中线，BE交AC于E，交AD于F，且AE＝EF.求证：AC＝BF.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在长度为1个单位长度的小正方形组成的正方形网格中，点A、B、C在小正方形的顶点上．

    （1）在图中画出与△ABC关于直线l成轴对称的△AB′C′；

    （2）在直线l上找一点P，使PB′+PC的长最短；

    （3）若△ACM是以AC为腰的等腰三角形，点M在小正方形的顶点上．这样的点M共有　 　个．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，已知正比例函数y=2x与反比例函数y=（k＞0）的图象交于A、B两点，且点A的横坐标为4，

    （1）求k的值；

    （2）根据图象直接写出正比例函数值小于反比例函数值时x的取值范围；

    （3）过原点O的另一条直线l交双曲线y=（k＞0）于P、Q两点（P点在第一象限），若由点A、P、B、Q为顶点组成的四边形面积为224，求点P的坐标．

    查看答案和解析>>

    同步练习册答案