
【题目】(阅读理解)
课外兴趣小组活动时,老师提出了如下问题:

如图1,△ABC中,若AB=8,AC=6,求BC边上的中线AD的取值范围.小明在组内经过合作交流,得到了如下的解决方法:延长AD到点E,使DE=AD,请根据小明的方法思考:
(1)由已知和作图能得到△ADC≌△EDB的理由是_____.
A.SSS B.SAS C.AAS D.HL
(2)求得AD的取值范围是______.
A.6<AD<8 B.6≤AD≤8 C.1<AD<7 D.1≤AD≤7
(感悟)
解题时,条件中若出现“中点”“中线”字样,可以考虑延长中线构造全等三角形,把分散的已知条件和所求证的结论集合到同一个三角形中.
(问题解决)
(3)如图2,AD是△ABC的中线,BE交AC于E,交AD于F,且AE=EF.求证:AC=BF.
【答案】(1)B;(2)C;(3)证明见解析.
【解析】
(1)根据AD=DE,∠ADC=∠BDE,BD=DC推出△ADC和△EDB全等即可;
(2)根据全等得出BE=AC=6,AE=2AD,由三角形三边关系定理得出8﹣6<2AD<8+6,求出即可;
(3)延长AD到M,使AD=DM,连接BM,根据SAS证△ADC≌△MDB,推出BM=AC,∠CAD=∠M,根据AE=EF,推出∠CAD=∠AFE=∠BFD,求出∠BFD=∠M,根据等腰三角形的性质求出即可.
(1)解:在△ADC和△EDB中
 ,
,
∴△ADC≌△EDB(SAS),
故选:B;
(2)解:如图:
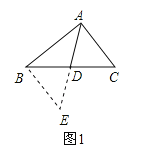
∵由(1)知:△ADC≌△EDB,
∴BE=AC=6,AE=2AD,
∵在△ABE中,AB=8,由三角形三边关系定理得:8﹣6<2AD<8+6,
∴1<AD<7,
故选:C.
(3)延长AD到M,使AD=DM,连接BM,
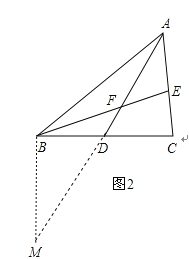
∵AD是△ABC中线,
∴CD=BD,
∵在△ADC和△MDB中

∴△ADC≌△MDB,
∴BM=AC,∠CAD=∠M,
∵AE=EF,
∴∠CAD=∠AFE,
∵∠AFE=∠BFD,
∴∠BFD=∠CAD=∠M,
∴BF=BM=AC,
即AC=BF.


 暑假衔接教材期末暑假预习武汉出版社系列答案
暑假衔接教材期末暑假预习武汉出版社系列答案 假期作业暑假成长乐园新疆青少年出版社系列答案
假期作业暑假成长乐园新疆青少年出版社系列答案科目:初中数学 来源: 题型:
【题目】如图,在 Rt△ABC 中,∠ACB=90°,BC=5,点 P 在边 AB 上,连接 CP.将△BCP 沿直线CP 翻折后,点 B 恰好落在边 AC 的中点处,则点 P 到 AC 的距离是( )

A. 2.5 B. ![]() C. 3.5 D.
C. 3.5 D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】王强同学用10块高度都是2cm的相同长方体小木块,垒了两堵与地面垂直的木墙,木墙之间刚好可以放进一个等腰直角三角板(AC=BC,∠ACB=90°),点C在DE上,点A和B分别与木墙的顶端重合,则两堵木墙之间的距离为______cm.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,∠AOB内一点P,P1,P2分别P是关于OA、OB的对称点,P1P2交OA于M,交OB于N,若P1P2=6cm,则△PMN的周长是( )

A.3cmB.4cmC.5cmD.6cm
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若等腰三角形腰长为2,有一个内角为80°,则它的底边长上的高为__.(精确到0.01,参考数据:sin50°≈0.766;sin80°≈0.985)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2019年暑假期间,某学校计划租用8辆客车送280名师生参加社会实践活动,现有甲、乙两种客车,它们的载客量和租金如表,设租用甲种客车x辆,租车总费用为w元.
甲种客车 | 乙种客车 | |
载客量(人/辆) | 30 | 40 |
租金(元/辆) | 270 | 320 |
(1)求出w(元)与x(辆)之间函数关系式,并直接写出自变量x的取值范围;
(2)选择怎样的租车方案所需的费用最低?最低费用多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC、△FGH中,D、E两点分别在AB、AC上,F点在DE上,G、H两点在BC上,且DE∥BC,FG∥AB,FH∥AC,若BG:GH:HC=4:6:5,则△ADE与△FGH的面积比为何?( )

A. 2:1 B. 3:2 C. 5:2 D. 9:4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知点A D C F在同一直线上,AB=DE,AD=CF,添加下列条件后,仍不能判断△ABC≌△DEF的是 ( )

A. BC=EFB. ∠A=∠EDFC. AB∥DED. ∠BCA=∠F
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,∠ABC=90°,AC=AD,M,N分别为AC,CD的中点,连接BM,MN,BN.∠BAD=60°,AC平分∠BAD,AC=2,BN的长为_____.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com