
����Ŀ��2019������ڼ䣬ijѧУ�ƻ�����8���ͳ���280��ʦ���μ����ʵ��������мס������ֿͳ������ǵ��ؿ������������������ü��ֿͳ�x������ܷ���ΪwԪ��
���ֿͳ� | ���ֿͳ� | |
�ؿ�������/���� | 30 | 40 |
���Ԫ/���� | 270 | 320 |
��1�����w��Ԫ����x������֮�亯����ϵʽ����ֱ��д���Ա���x��ȡֵ��Χ��
��2��ѡ�����������������ķ�����ͣ���ͷ��ö���Ԫ��
���𰸡���1��![]() ��
��![]() ��xΪ����������2�����ü��ֿͳ�4�����������ֿͳ�4��������ķ�����ͣ�Ϊ2360Ԫ��
��xΪ����������2�����ü��ֿͳ�4�����������ֿͳ�4��������ķ�����ͣ�Ϊ2360Ԫ��
��������
��1���������������ͳ�����=��ܷ����г����̼��ɣ����ݳ������ܳ����ƻ�����8��Ҫ�����ؿ��������ڵ���280���г�����ʽ��⼴�ɣ�
��2�����ݣ�1���еó��ı���ʽ�ж�w��x���������С���ٸ����Ա���x��ȡֵ��Χȡ���ֵ��⼴��.
�⣺��1�������ü��ֿͳ�x�������������ֿͳ�![]() ����
����
������ɵó�![]()
�������֪��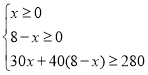
���![]() ��x����
��x����
���Ա���x��ȡֵ��ΧΪ��![]() ��xΪ������
��x������
��2����![]() ��x��ϵ��
��x��ϵ��![]() ��
��
��w��x�����������
�൱xȡ���ֵʱ��![]() ʱ��w��ֵ��С��
ʱ��w��ֵ��С��
����СֵΪ![]() Ԫ��
Ԫ��
�����ü��ֿͳ�4�����������ֿͳ�4��������ķ�����ͣ�Ϊ2360Ԫ��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ,��ƽ��ֱ������ϵ��,![]() �Ķ�������ֱ�ΪA(2��3)��B (1��1)��C(2��1)
�Ķ�������ֱ�ΪA(2��3)��B (1��1)��C(2��1)

(1)����![]() ����
����![]() ��ԳƵ�
��ԳƵ�![]() ,��д����
,��д����![]() ������Ϊ_________
������Ϊ_________
(2)��![]() ����ƽ��4����λ���ȵõ�
����ƽ��4����λ���ȵõ�![]() ,ֱ��д����
,ֱ��д����![]() ������Ϊ_________
������Ϊ_________
(3)ֱ��д����B����ֱ��n(ֱ��n�ϸ���������궼Ϊ-1)�ԳƵ�B'������Ϊ________
(4)��![]() ������һ��P��ʹPA+PB��ֵ��С�����P���λ��(������ͼ�ۼ�)
������һ��P��ʹPA+PB��ֵ��С�����P���λ��(������ͼ�ۼ�)
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����C��E�ֱ���ֱ��AB��DF�ϣ�С����֪����ACE�͡�DEC�Ƿ���������û�д���������ֻ����һ�����ǰ壬��������������һ���취����������CF�����ҳ�CF���е�O��Ȼ������EO���ӳ�EO��ֱ��AB�ཻ�ڵ�B������������������EO��BO��������ó����ۣ���ACE�͡�DEC������������������BC��EF.С�����뷨����Ϊʲô��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ҹ��Ŵ���ѧ�����ഴ�ºͷ�չ��λ������ǰ�У���������ѧ����������ġ�������������һ���У�����ͼ�������ν��Ͷ���ʽ��a+b��n��չ��ʽ�ĸ���ϵ�����������γ�Ϊ�������������

�������������������㣨a+b��10��չ��ʽ�е������ϵ��Ϊ��������
A. 2018 B. 2017 C. 55 D. 45
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����Ķ����⣩
������ȤС��ʱ����ʦ������������⣺

��ͼ1����ABC�У���AB��8��AC��6����BC���ϵ�����AD��ȡֵ��Χ.С�������ھ��������������õ������µĽ���������ӳ�AD����E��ʹDE��AD�������С���ķ���˼����
(1)����֪����ͼ�ܵõ���ADC�ա�EDB��������_____.
A.SSS B.SAS C.AAS D.HL
(2)���AD��ȡֵ��Χ��______.
A.6��AD��8 B.6��AD��8 C.1��AD��7 D.1��AD��7
������
����ʱ�����������������е��������������������Կ����ӳ����߹���ȫ�������Σ��ѷ�ɢ����֪����������֤�Ľ��ۼ��ϵ�ͬһ����������.
����������
(3)��ͼ2��AD�ǡ�ABC�����ߣ�BE��AC��E����AD��F����AE��EF.��֤��AC��BF.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ڡ�ABC�У���D��AB�ߵ��е㣬����D����AB�Ĵ���l��E��l������һ�㣬��AC=5��BC=8�����AEC���ܳ���СֵΪ______��
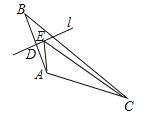
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ڳ���Ϊ1����λ���ȵ�С��������ɵ������������У���A��B��C��С�����εĶ����ϣ�

��1����ͼ�л������ABC����ֱ��l����ԳƵġ�AB��C�䣻
��2����ֱ��l����һ��P��ʹPB��+PC�ij���̣�
��3������ACM����ACΪ���ĵ��������Σ���M��С�����εĶ����ϣ������ĵ�M������ ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���Ķ����в��ϣ��������
������ͼ��
���壺��ij��ͼ�οɷָ�Ϊ���ɸ����������Ƶ�ͼ�Σ�������ͼ����������ͼ�Σ����磺������ABCD�У���E��F��G��H�ֱ���AB��BC��CD��DA�ߵ��е㣬����EG��HF���ڵ�O����֪�ָ�ɵ��ĸ��ı���AEOH��EBFO��OFCG��HOGD��Ϊ�����Σ�����ԭ���������ƣ�����������������ͼ�Σ�
����
��1��ͼ1��������ABCD�ָ�ɵ��ĸ�С�������У�ÿ����������ԭ�����ε����Ʊ�Ϊ�� ����
��2����ͼ2����֪��ABC�У���ACB=90�㣬AC=4��BC=3��С��������ABCҲ�ǡ�������ͼ�Ρ�������˼·�ǣ�����C��CD��AB�ڵ�D����CD����ABC�ָ��2�������Լ����Ƶ�Сֱ�������Σ���֪��ACD�ס�ABC������ACD����ABC�����Ʊ�Ϊ�� ����
��3������һ������ABCD��������ͼ�Σ����г�AD=a����AB=b��a��b����
�������A��B��������ѡһ��������ѡ���� ���⣮
A������ͼ3��1����������ABCD����ָ������ȫ�Ⱦ��Σ�����ԭ���ζ����ƣ���a=�� �����ú�b��ʽ�ӱ�ʾ����
����ͼ3��2��������ABCD����ָ��n��ȫ�Ⱦ��Σ�����ԭ���ζ����ƣ���a=�� �����ú�n��b��ʽ�ӱ�ʾ����
B������ͼ4��1����������ABCD������ָ��2��ȫ�Ⱦ��Σ��ٽ�ʣ��IJ��ֺ���ָ��3��ȫ�Ⱦ��Σ��ҷָ�õ��ľ�����ԭ���ζ����ƣ���a=�� �����ú�b��ʽ�ӱ�ʾ����
����ͼ4��2����������ABCD������ָ��m��ȫ�Ⱦ��Σ��ٽ�ʣ��IJ��ֺ���ָ��n��ȫ�Ⱦ��Σ��ҷָ�õ��ľ�����ԭ���ζ����ƣ���a=�� �����ú�m��n��b��ʽ�ӱ�ʾ����

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ABCD�У�E��BC���е㣬����AE���ӳ���DC���ӳ����ڵ�F��

��1����֤��AB=CF��
��2������DE����AD=2AB����֤��DE��AF��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com