
【题目】王强同学用10块高度都是2cm的相同长方体小木块,垒了两堵与地面垂直的木墙,木墙之间刚好可以放进一个等腰直角三角板(AC=BC,∠ACB=90°),点C在DE上,点A和B分别与木墙的顶端重合,则两堵木墙之间的距离为______cm.

【答案】20
【解析】
根据题意可得AC=BC,∠ACB=90°,AD⊥DE,BE⊥DE,进而得到∠ADC=∠CEB=90°,再根据等角的余角相等可得∠BCE=∠DAC,再证明△ADC≌△CEB即可,利用全等三角形的性质进行解答.
解:由题意得:AC=BC,∠ACB=90°,AD⊥DE,BE⊥DE,
∴∠ADC=∠CEB=90°,
∴∠ACD+∠BCE=90°,∠ACD+∠DAC=90°,
∴∠BCE=∠DAC,
在△ADC和△CEB中,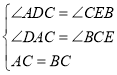 ,
,
∴△ADC≌△CEB(AAS);
由题意得:AD=EC=6cm,DC=BE=14cm,
∴DE=DC+CE=20(cm),
答:两堵木墙之间的距离为20cm.
故答案是:20.


 新思维假期作业暑假吉林大学出版社系列答案
新思维假期作业暑假吉林大学出版社系列答案 蓝天教育暑假优化学习系列答案
蓝天教育暑假优化学习系列答案科目:初中数学 来源: 题型:
【题目】如图,分别以Rt△ABC的斜边AB、直角边AC为边向外作等边△ABD和△ACE,F为AB中点,连接DF、EF,DE、EF与AC交于点O,DE与AB交于点G,连接OG,若∠BAC=30°,下列结论:①△DBF≌△EFA;②AD=AE;③EF⊥AC;④AD=4AG;⑤△AOG与△EOG的面积比为1:4.其中正确的结论的序号是_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,完成下列推理过程:
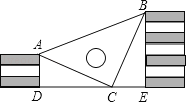
如图所示,点E在△ABC外部,点D在BC边上,DE交AC于F,若∠1=∠3,∠E=∠C,AE=AC,求证:△ABC≌△ADE.

证明:∵ ∠E=∠C(已知),
∠AFE=∠DFC(_________________),
∴∠2=∠3(______________________),
又∵∠1=∠3(_________________),
∴ ∠1=∠2(等量代换),
∴__________+∠DAC= __________+∠DAC(______________________),
即∠BAC =∠DAE,
在△ABC和△ADE中
∵ 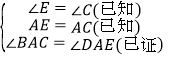
∴△ABC≌△ADE(_________________).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,在矩形ABCD中,E是BC边一点,DE平分∠ADC,EF∥DC角AD边于点F,连结BD.
(1)求证:四边形EFCD是正方形;
(2)若BE=1,ED=2![]() ,求BD的长.
,求BD的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点C、E分别在直线AB、DF上,小华想知道∠ACE和∠DEC是否互补,但是他没有带量角器,只带了一副三角板,于是他想了这样一个办法:首先连结CF,再找出CF的中点O,然后连结EO并延长EO和直线AB相交于点B,经过测量,他发现EO=BO,因此他得出结论:∠ACE和∠DEC互补,而且他还发现BC=EF.小华的想法对吗?为什么?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在学校开展的数学活动课上,小明和小刚制作了一个正三楼锥(质量均匀,四个面完全相同),并在各个面上分别标记数字1,2,3,4,游戏规则如下每人投掷三棱锥两次,并记录底面的数字,如果两次所掷数字的和为单数,那么算小明赢,如果两欢所掷数字的和为偶数,那么算小明赢;
(1)请用列表或者面树状围的方法表示上述游戏中的所有可能结果.
(2)请分别隶出小明和小刚能赢的概率,并判新游戏的公平性.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(阅读理解)
课外兴趣小组活动时,老师提出了如下问题:

如图1,△ABC中,若AB=8,AC=6,求BC边上的中线AD的取值范围.小明在组内经过合作交流,得到了如下的解决方法:延长AD到点E,使DE=AD,请根据小明的方法思考:
(1)由已知和作图能得到△ADC≌△EDB的理由是_____.
A.SSS B.SAS C.AAS D.HL
(2)求得AD的取值范围是______.
A.6<AD<8 B.6≤AD≤8 C.1<AD<7 D.1≤AD≤7
(感悟)
解题时,条件中若出现“中点”“中线”字样,可以考虑延长中线构造全等三角形,把分散的已知条件和所求证的结论集合到同一个三角形中.
(问题解决)
(3)如图2,AD是△ABC的中线,BE交AC于E,交AD于F,且AE=EF.求证:AC=BF.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知点A(1,a)是反比例函数![]() 的图象上一点,直线
的图象上一点,直线![]() 与反比例函数
与反比例函数![]() 的图象的交点为点B、D,且B(3,﹣1),求:
的图象的交点为点B、D,且B(3,﹣1),求:
(1)求反比例函数的解析式;
(2)求点D坐标,并直接写出y1>y2时x的取值范围;
(3)动点P(x,0)在x轴的正半轴上运动,当线段PA与线段PB之差达到最大时,求点P的坐标.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com