
【题目】如图,在四边形ABCD中,∠ABC=90°,AC=AD,M,N分别为AC,CD的中点,连接BM,MN,BN.∠BAD=60°,AC平分∠BAD,AC=2,BN的长为_____.

【答案】![]()
【解析】分析:根据三角形中位线定理得MN=![]() AD,根据直角三角形斜边中线定理得BM=
AD,根据直角三角形斜边中线定理得BM=![]() AC,从而可证MN=BM,;再由∠BMN=90°,根据BN2=BM2+MN2即可解决问题.
AC,从而可证MN=BM,;再由∠BMN=90°,根据BN2=BM2+MN2即可解决问题.
详解:在△CAD中,∵M、N分别是AC、CD的中点,
∴MN∥AD,MN=![]() AD,
AD,
在Rt△ABC中,∵M是AC中点,
∴BM=![]() AC,
AC,
∵AC=AD,
∴MN=BM,
∵∠BAD=60°,AC平分∠BAD,
∴∠BAC=∠DAC=30°,
∴BM=![]() AC=AM=MC,
AC=AM=MC,
∴∠BMC=∠BAM+∠ABM=2∠BAM=60°,
∵MN∥AD,
∴∠NMC=∠DAC=30°,
∴∠BMN=∠BMC+∠NMC=90°,
∴BN2=BM2+MN2,
∴MN=BM=![]() AC=1,
AC=1,
∴BN=![]() .
.
故答案为:![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】已知△ABC,分别以BC,AB,AC为边作等边三角形BCE,ACF,ABD
(1)若存在四边形ADEF,判断它的形状,并说明理由.
(2)存在四边形ADEF的条件下,请你给△ABC添个条件,使得四边形ADEF成为矩形,并说明理由.
(3)当△ABC满足什么条件时四边形ADEF不存在.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2018年河南中招体育考试测试时间将定于4月1日开始进行,光明中学为了了解本校九年级全体学生体育训练的成效,在校内提前进行了体育模拟测试,并对九级(1)班的休育模拟成绩按A、B、C、D四个等级进行统计,井将统计结果绘制如下两幅统计图,请你结合图中所给信息解答下列问题:(说明:A级:65 分~70 分;B级:60分~65 分;C 级:55 分~60分0;D级:55 分以下)
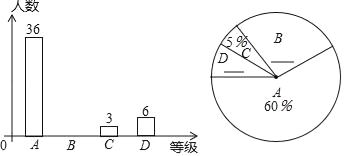
(1)九年级(1)班共有 人,D级学生所在的扇形圆心角的度数为 ;
(2)请补全条形统计图与扇形统计图;
(3)该班学生体育测试成绩的中位数落在等级 内;
(4)若该校九年级学生共有800人,请你估计这次考试中A级和B级的学生共有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明从家去体育场锻炼,同时,妈妈从体育场以50米/分的速度回家,小明到体育场后发现要下雨,立即返回,追上妈妈后,小明以250米/分的速度回家取伞,立即又以250米/分的速度折回接妈妈,并一同回家.如图是两人离家的距离y(米)与小明出发的时间x(分)之间的函数图像.
(注:小明和妈妈始终在同一条笔直的公路上行走,图像上A、C、D三点在一条直线上)
(1)求线段BC的函数表达式;
(2)求点D坐标;
(3)当 x的值为 时,小明与妈妈相距1 500米.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校七年级1至4班计划每班购买数量相同的图书布置班级读书角,但是由于种种原因,实际购书量与计划有出入,下表是实际购书情况:
班级 | 1班 | 2班 | 3班 | 4班 |
实际购买量(本) | a | 33 | c | 21 |
实际购买量与计划购数量的差值(本) | +12 | b | -8 | -9 |
(1) 直接写出a=__________,b=__________,c=__________
(2) 根据记录的数据可知4个班实际购书共_________本
(3) 书店给出一种优惠方案:一次购买不少于15本,其中2本书免费.若每本书售价为30元,请计算这4个班整体购书的最低总花费是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】体育器材室有A、B两种型号的实心球,1只A型球与1只B型球的质量共7千克,3只A型球与1只B型球的质量共13千克.
(1)每只A型球、B型球的质量分别是多少千克?
(2)现有A型球、B型球的质量共17千克,则A型球、B型球各有多少只?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若正比例函数y=kx(k≠0)的图象经过点P(2,3),则该函数的图象经过的点是( )
A.(3,2)B.(1,6)C.(2,3)D.(1,6)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,Rt△ABO的两直角边OA、OB分别在x轴的负半轴和y轴的正半轴上,O为坐标原点,A、B两点的坐标分别为(﹣3,0)、(0,4),抛物线![]() 经过点B,且顶点在直线x=
经过点B,且顶点在直线x=![]() 上.
上.

(1)求抛物线对应的函数关系式;
(2)若把△ABO沿x轴向右平移得到△DCE,点A、B、O的对应点分别是D、C、E,当四边形ABCD是菱形时,试判断点C和点D是否在该抛物线上,并说明理由;
(3)在(2)的条件下,连接CD,与抛物线的对称轴交于点P,若点M是线段OB上的一个动点(点M与点O、B不重合),过点M作MN∥BD交x轴于点N,连接PM、PN,设OM的长为t,△PMN的面积为S,求出S和t的函数关系式,并写出自变量t的取值范围,S是否存在最大值?若存在,求出最大值和此时M点的坐标;若不存在,说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com