
����Ŀ����ͼ��Rt��ABO����ֱ�DZ�OA��OB�ֱ���x��ĸ������y����������ϣ�OΪ����ԭ�㣬A��B���������ֱ�Ϊ����3��0������0��4����������![]() ������B���Ҷ�����ֱ��x=
������B���Ҷ�����ֱ��x=![]() �ϣ�
�ϣ�

��1���������߶�Ӧ�ĺ�����ϵʽ��
��2�����ѡ�ABO��x������ƽ�Ƶõ���DCE����A��B��O�Ķ�Ӧ��ֱ���D��C��E�����ı���ABCD������ʱ�����жϵ�C�͵�D�Ƿ��ڸ��������ϣ���˵�����ɣ�
��3���ڣ�2���������£�����CD���������ߵĶԳ��ύ�ڵ�P������M���߶�OB�ϵ�һ�����㣨��M���O��B���غϣ�������M��MN��BD��x���ڵ�N������PM��PN����OM�ij�Ϊt����PMN�����ΪS�����S��t�ĺ�����ϵʽ����д���Ա���t��ȡֵ��Χ��S�Ƿ�������ֵ�������ڣ�������ֵ�ʹ�ʱM������ꣻ�������ڣ�˵�����ɣ�
���𰸡���1��![]() ��2����C�͵�D������������������3����t=
��2����C�͵�D������������������3����t=![]() ʱ��Sȡ���ֵ��
ʱ��Sȡ���ֵ��![]() ����ʱ����M������Ϊ��0��
����ʱ����M������Ϊ��0��![]() ��
��
��������������(1)��ͨ����B��0��4���Լ������ߵĶԳ��ᣬ���������ϵʽ��(2)��ͨ�����ɶ����������������C��D��������꣬���뺯����ϵʽ��֤��(3)��ͨ��C��D��������꣬���ֱ��CD��Ӧ�ĺ�����ϵʽ���Ӷ������P�����꣬ͨ����OMN�ס�OBD���ON=![]() ����ͨ��������S��t�ĺ�����ϵʽ���Ӷ�������ֵ��M������꣮
����ͨ��������S��t�ĺ�����ϵʽ���Ӷ�������ֵ��M������꣮
��⣺��1����������y=![]() ������B��0��4����c=4��
������B��0��4����c=4��
�������ߵĶԳ���Ϊ![]() ���ੁ
���ੁ![]() =��
=��![]() ����b=��
����b=��![]() ��
��
����������ϵʽΪ![]() ��
��
��2����Rt��ABO�У�OA=3��OB=4����AB=5�����ı���ABCD�����Σ���BC=CD=DA=AB=5��
��C��D���������ֱ��ǣ�5��4������2��0���� ��x=5ʱ��y=![]() ��
��
��x=2ʱ��y=![]() �� ���C�͵�D���������������ϣ�
�� ���C�͵�D���������������ϣ�
��3����ֱ��CD��Ӧ�ĺ�����ϵʽΪy=kx+b�� ��![]() ����ã�
����ã�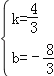 ����
����![]() ��
��
��![]() ʱ��y
ʱ��y![]() ����P��
����P��![]() ���� ��MN��BD�� ���OMN�ס�OBD��
���� ��MN��BD�� ���OMN�ס�OBD��
��![]() ��
�� ![]() ��ON=
��ON=![]() �� ��Գ��ύx�ڵ�F��
�� ��Գ��ύx�ڵ�F��
��![]() =
=![]() ��PF+OM��OF=
��PF+OM��OF=![]() ����
����![]() +t����
+t����![]() �� ��
�� ��![]() ��
��
![]() �� S��PMN=
�� S��PMN=![]() (0��t��4)��
(0��t��4)��
a=![]() ��0�������߿������£�S�������ֵ�� ��S��PMN=
��0�������߿������£�S�������ֵ�� ��S��PMN=![]() ��
��
�൱t=![]() ʱ��Sȡ���ֵ��
ʱ��Sȡ���ֵ��![]() ����ʱ����M������Ϊ��0��
����ʱ����M������Ϊ��0��![]() ����
����



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ�����ı���ABCD�У���ABC=90�㣬AC=AD��M��N�ֱ�ΪAC��CD���е㣬����BM��MN��BN����BAD=60�㣬ACƽ�֡�BAD��AC=2��BN�ij�Ϊ_____��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������ABC�У���C=90������B=30������AΪԲ�ģ����ⳤΪ�뾶�����ֱ�AB��AC�ڵ�M��N���ٷֱ���M��NΪԲ�ģ�����![]() MN�ij�Ϊ�뾶�������������ڵ�P������AP���ӳ���BC�ڵ�D��������˵������ȷ�ĸ����ǣ� ��
MN�ij�Ϊ�뾶�������������ڵ�P������AP���ӳ���BC�ڵ�D��������˵������ȷ�ĸ����ǣ� ��
��AD����BAC��ƽ���ߣ�
����ADC=60����
�۵�D��AB���д����ϣ�
��BD=2CD��

A��4 B��3 C��2 D��1
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵ�У�����y=2x+8��ͼ��ֱ�x�ᡢy����A��B���㣬����A��ֱ�߽�y���������ڵ�M���ҵ�MΪ�߶�OB���е㣮

��1����ֱ��AM�ĺ�������ʽ��
��2������ֱ��AM����һ��P��ʹ��S��ABP=S��AOB�������P�����꣮
��3������HΪ����ƽ��������һ�㣬������ƽ�����Ƿ���������ĵ�H��ʹ��A��B��M��HΪ������ı�����ƽ���ı��Σ������ڣ���ֱ��д�����е�H�����ꣻ�������ڣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ1����P.Q�ֱ��DZ߳�Ϊ4cm�ĵȱߡ�ABC��AB.BC�ϵĵ㣬��P�Ӷ���A��B��������Q�Ӷ���Bͬʱ������C���˶��������ǵ��ٶȶ�Ϊ1cm/s,

��1������AQ.CP���ڵ�M������P.Q�˶��Ĺ����У���ABQ���CAPȫ������˵�����ɣ�
��2����CMQ�仯�����仯����˵�����ɣ������䣬��������Ķ���.
��3��������PBQ��ֱ�������Σ�
��4����ͼ2������P.Q���˶����յ�����������AB.BC���˶���ֱ��AQ.CP����ΪM�����CMQ�仯�����仯����˵�����ɣ������䣬��������Ķ���.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����y��x2��bx��1��ͼ����(2��3)��
(1)����������ı���ʽ��
(2)��������ͼ��ָ��ͼ��Ķ������ꣻ
(3)�۲�ͼ��˵��y��x�������������仯�ģ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������˵���У���ȷ�ĸ����У�������
����ֱ֪�������ε����Ϊ2����ֱ�DZߵı�Ϊ1��2����б�߳�Ϊ![]() ��
��
��ֱ�������ε����߳�Ϊ![]() ����̱߳�Ϊ1������һ�߳�Ϊ
����̱߳�Ϊ1������һ�߳�Ϊ![]() ��
��
���ڡ�ABC�У�����A����B����C=1��5��6�����ABCΪֱ�������Σ�
�ܵ������������Ϊ12���ױ��ϵĸ�Ϊ4��������Ϊ5��
A. 1�� B. 2�� C. 3�� D. 4��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ڳ����� ABCD �У�����������״��С��ͬ�ij����Σ�����ߴ���ͼ��ʾ�� ��ͼ����Ӱ�������Ϊ�� ��

A. 44cm2B. 36cm2C. 96 cm2D. 84cm2
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij���ƻ���һ���뾶Ϊa��Բ�οյ������̻������������ַ���������һ����ͼ1����Բ�ĵȷ֣��м佨�������ഹֱ��դ������Ӱ������ֲ��ƺ����������������ͼ2��ʾ��Բ��������СԲ�뾶�պ�Ϊ��Բ�뾶��һ�룬��Ӱ������ֲ��ƺ.
(1)���ַ�������Ӱ���ֵ���������ƽ����(���������)��
(2)��ͼ3���ڷ������еĻ���������Χһ������Բ��������ֲ���ܣ���ͼ3������Բ���ܳ�֮��(���������).

�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com