
����Ŀ����ͼ����ƽ��ֱ������ϵ�У�����y=2x+8��ͼ��ֱ�x�ᡢy����A��B���㣬����A��ֱ�߽�y���������ڵ�M���ҵ�MΪ�߶�OB���е㣮

��1����ֱ��AM�ĺ�������ʽ��
��2������ֱ��AM����һ��P��ʹ��S��ABP=S��AOB�������P�����꣮
��3������HΪ����ƽ��������һ�㣬������ƽ�����Ƿ���������ĵ�H��ʹ��A��B��M��HΪ������ı�����ƽ���ı��Σ������ڣ���ֱ��д�����е�H�����ꣻ�������ڣ���˵�����ɣ�
���𰸡���1��y=x+4����2����P������Ϊ��-12��-8����4��8������3�����ڣ���-4��-4������-4��4����4��12����
��������
��1��ͨ������y=2x+8���A��M�������꣬�������������ֱ��AM�ĺ�������ʽ��
��2�����P�����꣬���յ�����ϵ��S��ABP=S��AOB�����������
��3�����H������Ϊ��m��n����Ȼ�����������������ۼ���.
��1����x=0ʱ��y=2x+8=8��
���B��������0��8����
��y=0ʱ��2x+8=0��
��ã�x=-4��
���A��������-4��0����
�ߵ�MΪ�߶�OB���е㣬
���M��������0��4����
��ֱ��AM�ĺ�������ʽΪy=kx+b��k��0����
��A��-4��0����B��0��4������y=kx+b���ã�![]() ��
��
��ã�![]() ��
��
��ֱ��AM�ĺ�������ʽΪy=x+4��
��2�����P��������x��x+4����
��S��ABP=S��AOB��
��![]() BM|xP-xA|=
BM|xP-xA|=![]() OAOB����
OAOB����![]() ��4��|x+4|=
��4��|x+4|=![]() ��4��8��
��4��8��
��ã�x1=-12��x2=4��
���P��������-12��-8����4��8����
��3�����ڣ� ��-4��-4������-4��4����4��12����
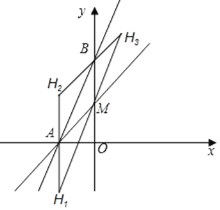
���H��������m��n����
������������ǣ���ͼ��ʾ����
�ٵ�AMΪ�Խ���ʱ��![]() ��
��
��ã�![]() ��
��
���H1��������-4��-4����
�ڵ�ABΪ�Խ���ʱ�� ![]() ��
��
��ã�![]() ��
��
���H2��������-4��4����
�۵�BMΪ�Խ���ʱ��![]() ��
��
��ã�![]() ��
��
���H3��������4��12����
����������������ƽ���ڴ��ڵ�H��ʹ��A��B��M��HΪ������ı�����ƽ���ı��Σ���H������Ϊ��-4��-4������-4��4����4��12����


 ǧ�������������ĩ�����Ծ�����ϵ�д�
ǧ�������������ĩ�����Ծ�����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪DC��FP����1����2����FED��28����AGF��80��FHƽ�֡�EFG��
(1)˵����DC��AB��
(2)���PFH�Ķ�����

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������ABCD�ڽ��ڡ�O����ͼ��ʾ�����ӻ�![]() ��ȡһ��E������DE��BE������D��DF��BE����O�ڵ�F������BF��AF����AF��DE�ཻ�ڵ�G����֤��
��ȡһ��E������DE��BE������D��DF��BE����O�ڵ�F������BF��AF����AF��DE�ཻ�ڵ�G����֤��

��1���ı���EBFD�Ǿ��Σ�
��2��DG=BE��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ƽ��ֱ������ϵ�У�����OABC��OC������x���ϣ���AOC=60����OA=60![]() ��������OABC�ڲ����߽缰������⣩��һ���P��x��y�����㣺x2��y2=90x��90y���ͳƸ��PΪ���õ�����������OABC�ڲ����õ����ĸ���Ϊ��������
��������OABC�ڲ����߽缰������⣩��һ���P��x��y�����㣺x2��y2=90x��90y���ͳƸ��PΪ���õ�����������OABC�ڲ����õ����ĸ���Ϊ��������
��ע����ν�����������ָ��ƽ��ֱ������ϵ�кᡢ�������Ϊ�����ĵ㣮��

A. 145 B. 146 C. 147 D. 148
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��С��ÿ������9ʱ�����г��뿪�ң�15ʱ�ؼң����������ҵľ���ʱ��ı仯�����

��1��ͼ���ʾ�����������Ĺ�ϵ���ĸ����Ա������ĸ����������
��2��10ʱ��13ʱ�����ֱ���Ҷ�Զ��
��3�������������Զ�ĵط�ʱʲôʱ�䣿��Ҷ�Զ��
��4��11ʱ��12ʱ����ʻ�˶���ǧ�ף�
��5�����������Զ�ĵط����ص�ƽ���ٶ��Ƕ��٣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ʾ��������ABCD�У�AB=4����BAD=120�㣬��AEFΪ�������Σ���E��F�ֱ������εı�BC��CD�ϻ�������E��F����B��C��D�غϣ�����E��F��BC��CD�ϻ���ʱ������CEF��������ֵ��____��
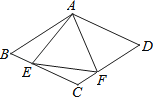
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����һ�ڼ䣬ij�̳��ƻ������ס���������Ʒ����֪��������Ʒ1��������Ʒ3������240Ԫ����������Ʒ2��������Ʒ1������130Ԫ��
��1����ס���������Ʒÿ���Ľ��۷ֱ��Ƕ���Ԫ��
��2���̳���������Ʒ��ÿ��40Ԫ���ۣ�����Ʒ��ÿ��90Ԫ���ۣ�Ϊ�����г������蹺���ס���������Ʒ��100�����Ҽ�����Ʒ������������������Ʒ������4������������������Ľ�����������ȷ���������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ABCD�ĶԽ���AC��BD�ཻ�ڵ�O��AC��AB��AB��2![]() ����AO��BO��2��3.
����AO��BO��2��3.

(1)��AC�ij���
(2)��ABCD�������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪����������y=![]() ��ͼ����ֱ��y=��x+b��������A��1��4�����Ҹ�ֱ����x��Ľ���ΪB��
��ͼ����ֱ��y=��x+b��������A��1��4�����Ҹ�ֱ����x��Ľ���ΪB��
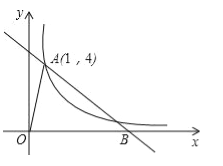
��1������������ֱ�ߵĽ���ʽ��
��2�����AOB�������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com