
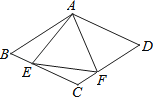
【题目】如图所示,在菱形ABCD中,AB=4,∠BAD=120°,△AEF为正三角形,点E、F分别在菱形的边BC、CD上滑动,且E、F不与B、C、D重合.当点E、F在BC、CD上滑动时,则△CEF的面积最大值是____.
【答案】![]()
【解析】解:如图,连接AC,∵四边形ABCD为菱形,∠BAD=120°,∠1+∠EAC=60°,∠3+∠EAC=60°,∴∠1=∠3,∵∠BAD=120°,∴∠ABC=60°,∴△ABC和△ACD为等边三角形,∴∠4=60°,AC=AB.
在△ABE和△ACF中,∵∠1=∠3,AC=AC,∠ABC=∠4,∴△ABE≌△ACF(ASA),∴S△ABE=S△ACF,∴S四边形AECF=S△AEC+S△ACF=S△AEC+S△ABE=S△ABC,是定值,作AH⊥BC于H点,则BH=2,∴S四边形AECF=S△ABC=![]() BCAH=
BCAH=![]() BC
BC![]() =
=![]() ,由“垂线段最短”可知:当正三角形AEF的边AE与BC垂直时,边AE最短,∴△AEF的面积会随着AE的变化而变化,且当AE最短时,正三角形AEF的面积会最小,又∵S△CEF=S四边形AECF﹣S△AEF,则此时△CEF的面积就会最大,∴S△CEF=S四边形AECF﹣S△AEF=
,由“垂线段最短”可知:当正三角形AEF的边AE与BC垂直时,边AE最短,∴△AEF的面积会随着AE的变化而变化,且当AE最短时,正三角形AEF的面积会最小,又∵S△CEF=S四边形AECF﹣S△AEF,则此时△CEF的面积就会最大,∴S△CEF=S四边形AECF﹣S△AEF=![]() ﹣
﹣![]() ×
×![]() ×
×![]() =
=![]() .
.
故答案为: ![]() .
.


 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案科目:初中数学 来源: 题型:
【题目】如图,在直角边分别为3和4的直角三角形中,每多作一条斜边上的高就增加一个三角形的内切圆,依次类推,图10中有10个直角三角形的内切圆,它们的面积分别记为![]() ,
,![]() ,
,![]() ,…,
,…, ![]() ,则
,则![]() = .
= .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,已知射线CB∥OA,∠C=∠OAB,
(1)求证:AB∥OC;
(2)如图2,E、F在CB上,且满足∠FOB=∠AOB,OE平分∠COF.
①当∠C=110°时,求∠EOB的度数.
②若平行移动AB,那么∠OBC :∠OFC的值是否随之发生变化?若变化,找出变
化规律;若不变,求出这个比值.


查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有这样一个问题:探究函数![]() 的图象与性质.小华根据学习函数的经验,对函数
的图象与性质.小华根据学习函数的经验,对函数![]() 的图象与性质进行了探究.下面是小华的探究过程,请补充完整:
的图象与性质进行了探究.下面是小华的探究过程,请补充完整:
(1)在函数![]() 中,自变量x的取值范围是________.
中,自变量x的取值范围是________.
x | … | -4 | -3 | -2 | -1 | 0 | 1 | 2 | 3 | 4 | … |
y | … | 5 | 4 | 3 | 2 | 1 | 0 | 1 | 2 | m | … |
①求m的值;
②在平面直角坐标系xOy中,描出以上表中各组对应值为坐标的点,并根据描出的点,画出该函数的图象.

(2)结合函数图象写出该函数的一条性质:________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,函数y=2x+8的图象分别交x轴、y轴于A、B两点,过点A的直线交y轴正半轴于点M,且点M为线段OB的中点.

(1)求直线AM的函数解析式.
(2)试在直线AM上找一点P,使得S△ABP=S△AOB,求出点P的坐标.
(3)若点H为坐标平面内任意一点,在坐标平面内是否存在这样的点H,使以A、B、M、H为顶点的四边形是平行四边形?若存在,请直接写出所有点H的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某学校随机抽取部分学生,调查每个月的零花钱消费额,数据整理成如下的统计表和如图①②所示的两幅不完整的统计图,已知图①中A,E两组对应的小长方形的高度之比为2:1请结合相关数据解答以下问题:
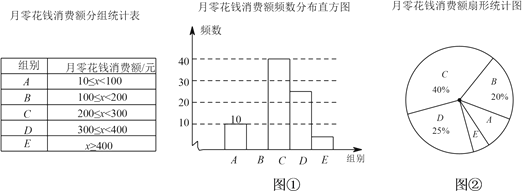
(1)本次调查样本的容量是______;
(2)补全频数分布直方图,并标明各组的频数;
(3)若该学校有2500名学生,请估计月消费零花钱不少于300元的学生的数量.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场有A、B两种商品,每件的进价分别为15元、35元.商场销售5件A商品和2件B商品,可获得利润45元;销售8件A商品和4件B商品,可获得利润80元.
(1)求A、B两种商品的销售单价;
(2)如果该商场计划购进A、B两种商品共80件,用于进货资金最多投入2 000元,但又要确保获利至少590元,请问有那几种进货方案?
查看答案和解析>>
科目:初中数学 来源: 题型:
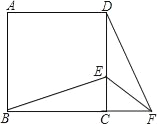
【题目】如图,正方形ABCD中,E为CD边上一点,F为BC延长线上一点,CE=CF.
(1)求证:△BCE≌△DCF;
(2)若∠BEC=60°,求∠EFD的度数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com