
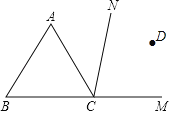
【题目】如图,CN是等边△ABC的外角∠ACM内部的一条射线,点A关于CN的对称点为D,连接AD,BD,CD,其中AD,BD分别交射线CN于点E,P.
(Ⅰ)依题意补全图形.
(Ⅱ)若∠ACN=α,求∠BDC的大小(用含α的式子表示).
(Ⅲ)若PA=x,PC=y,求PB的长度(用x,y的代数式表示).
【答案】(Ⅰ)补图见解析;(Ⅱ)∠BDC=60°﹣α;(Ⅲ)PB= x+y.
【解析】
(Ⅰ)根据题意画图即可;
(Ⅱ)根据对称得:CN是AD的垂直平分线,则CA=CD,然后根据等腰三角形的性质和等边三角形的性质可得结论;
(Ⅲ)作辅助线,在PB上截取PF使PF=PC,连接CF,PA.先证明△CPF是等边三角形,再证明△BFC≌△APC,则BF=PA,由此即可解决问题.
解:(Ⅰ)如图,
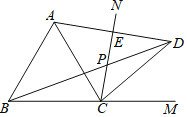
(Ⅱ) ∵点A与点D关于CN对称,
∴CN是AD的垂直平分线,
∴CA=CD,∠DCN=∠ACN=α,
∴∠ACD=2∠ACN=2α.
∵等边△ABC,
∴CA=CB,
∴CD=CB,
∴∠BDC=∠DBC.
∵∠ACB=60°.
∴∠BCD=∠ACB+∠ACD=60°+2α.
∴∠BDC=∠DBC=![]() (180°﹣∠BCD)=60°﹣α.
(180°﹣∠BCD)=60°﹣α.
(Ⅲ)在PB上截取PF使PF=PC,连接CF,PA
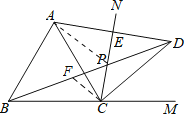
设∠ACN=α,
∵CA=CD,∠ACD=2α,
∴∠CDA=∠CAD=90°﹣α.
∵∠BDC=60°﹣α,
∴∠PDE=∠CDA﹣∠BDC=30°,
∵∠CPF=∠DPE=90°﹣∠PDE=60°.
∴△CPF是等边三角形.
∴CF=CP,∠PCF=60°,
∵∠PCF=∠ACB,
∴∠BCF=∠ACP,
∵CB=CA,CF=CP,
∴△BFC≌△APC(SAS),
∴BF=PA,
∴PB=PF+BF=PA+PC=x+y.


科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠C=90°,点P在AC上运动,点D在AB上,PD始终保持与PA相等,BD的垂直平分线交BC于点E,交BD于点F,连接DE.

(1)判断DE与DP的位置关系,并说明理由;
(2)若AC=6,BC=8,PA=2,求线段DE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随着中国传统节日“端午节”的临近,东方红商场决定开展“欢度端午,回馈顾客”的让利促销活动,对部分品牌粽子进行打折销售,其中甲品牌粽子打八折,乙品牌粽子打七五折,已知打折前,买6盒甲品牌粽子和3盒乙品牌粽子需660元;打折后,买50盒甲品牌粽子和40盒乙品牌粽子需要5200元.
(1)打折前甲、乙两种品牌粽子每盒分别为多少元?
(2)阳光敬老院需购买甲品牌粽子80盒,乙品牌粽子100盒,问打折后购买这批粽子比不打折节省了多少钱?
查看答案和解析>>
科目:初中数学 来源: 题型:
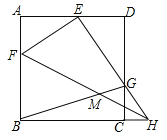
【题目】正方形ABCD中,F是AB上一点,H是BC延长线上一点,连接FH,将△FBH沿FH翻折,使点B的对应点E落在AD上,EH与CD交于点G,连接BG交FH于点M,当GB平分∠CGE时,BM=2![]() ,AE=8,则ED=______.
,AE=8,则ED=______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图a是一个长为2m,宽为2n的长方形,沿图中虚线用剪刀平均分成四块小长方形,然后按图b的形状,拼成一个正方形.

(1)图b中的阴影部分面积为 ;
观察图b,请你写出三个代数式![]() ,
,![]() ,mn之间的等量关系是 ;
,mn之间的等量关系是 ;
(3)若x+y=﹣6,xy=2.75,利用提供的等量关系计算:x﹣y= ;
(4)实际上有许多代数恒等式可以用图形的面积来表示,如图C,它表示了2![]() +3mn+
+3mn+![]() =(m+n)(2m+n),试画出一个几何图形的面积是
=(m+n)(2m+n),试画出一个几何图形的面积是![]() +4ab+3
+4ab+3![]() ,并能利用这个图形将
,并能利用这个图形将![]() +4ab+3
+4ab+3![]() 进行因式分解.
进行因式分解.
查看答案和解析>>
科目:初中数学 来源: 题型:
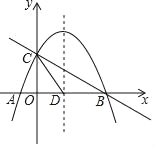
【题目】如图,抛物线y=﹣![]() x2+mx+n与x轴交于A、B两点,与y轴交于点C,抛物线的对称轴交x轴于点D,已知A(﹣1,0),C(0,2),点E是线段BC上的一个动点,过点E作x轴的垂线与抛物线相交于点F,当四边形CDBF的面积最大时,E点的坐标为_____.
x2+mx+n与x轴交于A、B两点,与y轴交于点C,抛物线的对称轴交x轴于点D,已知A(﹣1,0),C(0,2),点E是线段BC上的一个动点,过点E作x轴的垂线与抛物线相交于点F,当四边形CDBF的面积最大时,E点的坐标为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有关部门从甲、乙两个城市所有的自动售货机中分别随机抽取了16台,记录下某一天各自的销售情况(单位:元):
甲:18,8,10,43,5,30,10,22,6,27,25,58,14,18,30,41
乙:22,31,32,42,20,27,48,23,38,43,12,34,18,10,34,23
小强用如图所示的方法表示甲城市16台自动售货机的销售情况.
(1)请你仿照小强的方法将乙城市16台自动售货机的销售情况表示出来;
(2)请你观察图1,你能从图1中获取哪些信息?(至少写出两条不同类型信息)
(3)小芳用图2的条形统计图表示甲城市16台自动售货机的销售情况,请你观察图2,你能从图2中获取哪些信息?(至少写出两条不同类型信息)
(4)如果收集到的数据很多,例如有200个,你认为图1和图2这两种统计图用哪一种更能直观的反映这些数据分布的大致情况?请说明理由.


查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=BC,以AB为直径的⊙O交BC于点D,交AC于点F,过点C作CE∥AB,与过点A的切线相交于点E,连接AD.
(1)求证:AD=AE;
(2)若AB=6,AC=4,求AE的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在 Rt△ABC 中,∠ACB=90°,BC=5,点 P 在边 AB 上,连接 CP.将△BCP 沿直线CP 翻折后,点 B 恰好落在边 AC 的中点处,则点 P 到 AC 的距离是( )

A. 2.5 B. ![]() C. 3.5 D.
C. 3.5 D. ![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com