
【题目】如图,抛物线y=﹣![]() x2+mx+n与x轴交于A、B两点,与y轴交于点C,抛物线的对称轴交x轴于点D,已知A(﹣1,0),C(0,2),点E是线段BC上的一个动点,过点E作x轴的垂线与抛物线相交于点F,当四边形CDBF的面积最大时,E点的坐标为_____.
x2+mx+n与x轴交于A、B两点,与y轴交于点C,抛物线的对称轴交x轴于点D,已知A(﹣1,0),C(0,2),点E是线段BC上的一个动点,过点E作x轴的垂线与抛物线相交于点F,当四边形CDBF的面积最大时,E点的坐标为_____.
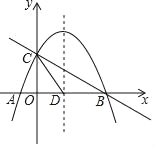
【答案】(2,1)
【解析】
由于四边形CDBF的面积等于△CDB的面积与△BCF的面积之和,当四边形CDBF的面积最大时,即△BCF最大,设点E的坐标为(x,y),利用点E的坐标表示出△BCF的面积即可求出点E的坐标.
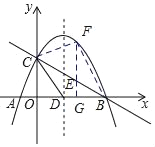
过点E作EG⊥x轴于点G,交抛物线于F,
将A(﹣1,0),C(0,2)代入y=﹣![]() x2+mx+n
x2+mx+n
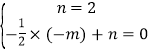
解得:
∴抛物线的解析式为:y=﹣![]() x2+
x2+![]() x+2
x+2
令y=0代入y=﹣![]() x2+
x2+![]() x+2,
x+2,
∴0=﹣![]() x2+
x2+![]() x+2
x+2
解得:x=﹣1或x=4
∴B(4,0)
∴OB=4
设直线BC的解析式为y=kx+b,
把B(4,0)和C(0,2)代入y=kx+b
∴![]()
解得: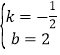
∴直线BC的解析式为:y=﹣![]() x+2,
x+2,
设E的坐标为:(x,﹣![]() x+2)
x+2)
∴F(x,﹣![]() x2+
x2+![]() x+2)
x+2)
∴EF=﹣![]() x2+
x2+![]() x+2﹣(﹣
x+2﹣(﹣![]() x+2)=﹣
x+2)=﹣![]() x2+2x,
x2+2x,
∴△BCF的面积为:![]() EFOB=2(﹣
EFOB=2(﹣![]() x2+2x)=﹣x2+4x=﹣(x﹣2)2+4
x2+2x)=﹣x2+4x=﹣(x﹣2)2+4
四边形CDBF的面积最大时,只需要△BCF的面积最大即可,
∴当x=2时,
△BCF的面积可取得最大值,
此时E的坐标为(2,1)
故答案是:(2,1).


 冲刺100分1号卷系列答案
冲刺100分1号卷系列答案 期末好成绩系列答案
期末好成绩系列答案科目:初中数学 来源: 题型:
【题目】在学校开展的数学活动课上,小明和小刚制作了一个正三楼锥(质量均匀,四个面完全相同),并在各个面上分别标记数字1,2,3,4,游戏规则如下每人投掷三棱锥两次,并记录底面的数字,如果两次所掷数字的和为单数,那么算小明赢,如果两欢所掷数字的和为偶数,那么算小明赢;
(1)请用列表或者面树状围的方法表示上述游戏中的所有可能结果.
(2)请分别隶出小明和小刚能赢的概率,并判新游戏的公平性.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一透明圆柱形无盖容器高12cm,底面周长24cm,在杯口点B处有一滴蜂蜜,此时一只蚂蚁在杯外壁底部与蜂蜜相对的A处.

(1)若蜂蜜固定不动,求蚂蚁吃到蜂蜜所爬行的最短路线长;
(2)若该蚂蚁刚出发时发现B处的蜂蜜正以0.5cm/s的速度沿杯内壁下滑,它便沿最短路径在8秒钟时吃到了蜂蜜,求此蚂蚁爬行的平均速度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】探究题:![]() =___________,
=___________,![]() =___________,
=___________,![]() =___________,
=___________,
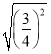 =_________,
=_________,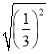 =__________,
=__________,![]() =___________,
=___________,
根据计算结果,回答:
(1)![]() 一定等于
一定等于![]() 吗?你发现其中的规律了吗?请你用数学语言描述出来。
吗?你发现其中的规律了吗?请你用数学语言描述出来。
(2)利用你总结的规律,计算:
①若![]() ,则
,则![]() =_____________;
=_____________;
②![]() =______________________;
=______________________;
查看答案和解析>>
科目:初中数学 来源: 题型:
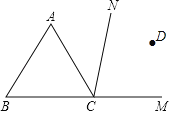
【题目】如图,CN是等边△ABC的外角∠ACM内部的一条射线,点A关于CN的对称点为D,连接AD,BD,CD,其中AD,BD分别交射线CN于点E,P.
(Ⅰ)依题意补全图形.
(Ⅱ)若∠ACN=α,求∠BDC的大小(用含α的式子表示).
(Ⅲ)若PA=x,PC=y,求PB的长度(用x,y的代数式表示).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(本小题满分10分)
如图,在□ABCD中,以点A为圆心,AB长为半径画弧交AD于点F;再分别以点B、F为圆心,大于![]() BF的相同长为半径画弧,两弧交于点P;连接AP并延长交BC于点E,连接EF,则所得四边形ABEF是菱形.
BF的相同长为半径画弧,两弧交于点P;连接AP并延长交BC于点E,连接EF,则所得四边形ABEF是菱形.
(1)根据以上尺规作图的过程,求证四边形ABEF是菱形;
(2)若菱形ABEF的周长为16,AE=4![]() ,求∠C的大小.
,求∠C的大小.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在等腰Rt△ABC中,∠BAC=90°,点E在AC上(且不与点A、C重合).在△ABC的外部作等腰Rt△CED,使∠CED=90°,连接AD,分别以AB,AD为邻边作平行四边形ABFD,连接AF.
(1)求证:△AEF是等腰直角三角形;
(2)如图2,将△CED绕点C逆时针旋转,当点E在线段BC上时,连接AE,求证:AF=![]() AE;
AE;
(3)如图3,将△CED绕点C继续逆时针旋转,当平行四边形ABFD为菱形,且△CED在△ABC的下方时,若AB=2![]() ,CE=2,求线段AE的长.
,CE=2,求线段AE的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对于一次函数![]() (k,b为常数),下表中给出5组自变量及其对应的函数值:
(k,b为常数),下表中给出5组自变量及其对应的函数值:
| …… | -1 | 0 | 1 | 2 | 3 | |
| …… | -2 | 1 | 4 | 8 | 10 | …… |
其中只有1个函数值计算有误,则这个错误的函数值是( )
A.1B.4C.8D.10
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,![]() 的顶点坐标分别为A(2,3)、B (1,1)、C(2,1)
的顶点坐标分别为A(2,3)、B (1,1)、C(2,1)

(1)画出![]() 关于
关于![]() 轴对称的
轴对称的![]() ,并写出点
,并写出点![]() 的坐标为_________
的坐标为_________
(2)将![]() 向左平移4个单位长度得到
向左平移4个单位长度得到![]() ,直接写出点
,直接写出点![]() 的坐标为_________
的坐标为_________
(3)直接写出点B关于直线n(直线n上各点的纵坐标都为-1)对称点B'的坐标为________
(4)在![]() 轴上找一点P,使PA+PB的值最小,标出P点的位置(保留画图痕迹)
轴上找一点P,使PA+PB的值最小,标出P点的位置(保留画图痕迹)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com