
如图,在等腰直角△ACB中,∠ACB=90°,O是斜边AB的中点,点D、E分别在直角边AC、BC上,且∠DOE=90°,DE交OC于点P.有下列结论:
①∠DEO=45°;②△AOD≌△COE;③S四边形CDOE= S△ABC;④OD2=OP•OC.
S△ABC;④OD2=OP•OC.
其中正确的结论序号为 .(把你认为正确的都写上)

①②③④
【解析】
试题分析:∵在等腰直角△ACB中,∠ACB=90°,O是斜边AB的中点,
∴∠A=∠B=∠ACO=°,OA=OC=OB,∠AOC=90°=∠DOE,
∴∠AOD=∠COE=90°-∠DOC,
在△AOD与△COE中,
 ,
,
∴△AOD≌△COE(ASA),
∴OD=OE,
∵∠EOD=90°,
∴∠DEO=45°,
∵△AOD≌△COE,∴S△AOD=S△COE,
∴S四边形CDOE=S△COD+S△COE=S△COD+S△AOD=S△AOC=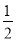 S△ABC,
S△ABC,
∵△DOE为等腰直角三角形,
∴∠DEO=45°.
∵∠DEO=∠OCE=45°,∠COE=∠COE,
∴△OEP∽△OCE,
∴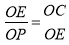 ,即OP•OC=OE2,
,即OP•OC=OE2,
即①②③④都正确;
故答案为:①②③④.
考点:全等三角形的判定与性质;等腰直角三角形;相似三角形的判定与性质.


科目:初中数学 来源:2013-2014学年山东省九年级第一次学业水平模拟考试数学试卷(解析版) 题型:选择题
如图所示,在平行四边形纸片上作随机扎针实验,针头扎在阴影区域内的概率为( )
(A) (B)
(B) (C)
(C)  (D)
(D)

查看答案和解析>>
科目:初中数学 来源:2013-2014学年山东省德州市九年级第一次模拟考试数学试卷(解析版) 题型:解答题
某宾馆有30个房间供游客住宿,当每个房间的房价为每天120元时,房间会全部住满.当每个房间每天的房价每增加10元时,就会有一个房间空闲.宾馆需对游客居住的每个房间每天支出20元的各种费用.根据规定,每个房间每天的房价不得高于210元.设每个房间的房价增加x元(x为10的正整数倍).
(1)设一天订住的房间数为y,直接写出y与x的函数关系式及自变量x的取值 范围;
(2)设宾馆一天的 利润为w元,求w与x的函数关系式;
(3)一天订住多少个房间时,宾馆的利润最大?最大利润是多少元?
查看答案和解析>>
科目:初中数学 来源:2013-2014学年山东省德州市九年级第一次模拟考试数学试卷(解析版) 题型:选择题
已知点M(1-2m,1-m)在第一象限,则m的取值范围在数轴上表示正确的是

查看答案和解析>>
科目:初中数学 来源:2013-2014学年山东省德州市中考一模数学试卷(解析版) 题型:解答题
某宾馆有30个房间供游客住宿,当每个房间的房价为每天120元时,房间会全部住满.当每个房间每天的房价每增加10元时,就会有一个房间空闲.宾馆需对游客居住的每个房间每天支出20元的各种费用.根据规定,每个房间每天的房价不得高于210元.设每个房间的房价增加x元(x为10的正整数倍).
(1)设一天订住的房间数为y,直接写出y与x的函数关系式及自变量x的取值范围;
(2)设宾馆一天的利润为w元,求w与x的函数关系式;
(3)一天订住多少个房间时,宾馆的利润最大?最大利润是多少元?
查看答案和解析>>
科目:初中数学 来源:2013-2014学年山东省德州市中考一模数学试卷(解析版) 题型:选择题
如图,已知小正方形ABCD的面积为1,把它的各边延长一倍得到新正方形A1B1C1D1;把正方形A1B1C1D1边长按原法延长一倍得到正方形A2B2C2D2;以此进行下去…,则正方形AnBnCnDn的面积为( )
A.( )n B.5n C.5n-1 D.5n+1
)n B.5n C.5n-1 D.5n+1

查看答案和解析>>
科目:初中数学 来源:2013-2014学年山东省德州市中考一模数学试卷(解析版) 题型:选择题
已知点M(1-2m,m-1)关于x轴的对称点在第一象限,则m的取值范围在数轴上表示正确的是( )
A.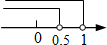 B.
B.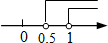 C.
C.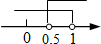 D.
D.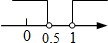
查看答案和解析>>
科目:初中数学 来源:2013-2014学年山东省临沂市九年级中考一模数学试卷(解析版) 题型:选择题
如图,在平面直角坐标系中,抛物线 经过平移得到抛物线
经过平移得到抛物线 ,其对称轴与两段抛物线所围成的阴影部分的面积为( )
,其对称轴与两段抛物线所围成的阴影部分的面积为( )
A.2 B.4 C.8 D.16

查看答案和解析>>
科目:初中数学 来源:2013-2014学年安徽省当涂县四校九年级上学期期末联考数学试卷(解析版) 题型:解答题
一船在A处测得北偏东45°方向有一灯塔B,船向正东方向以每小时20海里的速度航行1.5小时到达C处时,又观测到灯塔B在北偏东15°方向上,求此时航船与灯塔相距多少海里?

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com