
【题目】如图,⊙O是△ABC的外接圆,圆心O在AB上,M是OA上一点,过M作AB的垂线交BC的延长线于点E,过点C作⊙O的切线,交ME于点F. 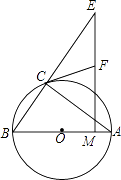
(1)求证:EF=CF;
(2)若∠B=2∠A,AB=4,且AC=CE,求BM的长.
【答案】
(1)证明:延长FC至H,如图所示:
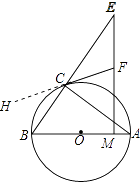
∵⊙O是△ABC的外接圆,圆心O在AB上,
∴AB是⊙O的直径,
∴∠ACB=90°,
∵EM⊥AB,
∴∠EMB=∠ACB=90°,
∵∠ABC=∠EBM,
∴△ABC∽△EMB,
∴∠CEF=∠CAB,
∵FC是⊙O的切线,
∴∠CAB=∠BCH,
∵∠BCH=∠ECF
∴∠CAB=∠ECF,
∴∠CEF=∠ECF,
∴EF=CF;
(2)解:∵∠ACB=90°,∠B=2∠A,
∴∠B=60°,∠A=30°,
在Rt△ABC中,∠ACB=90°,∠A=30°,AB=4,
∴BC= ![]() AB=2,AC=
AB=2,AC= ![]() BC=2
BC=2 ![]() ,
,
∵AC=CE,
∴CE=2 ![]() ,
,
∴BE=BC+CE=2+2 ![]() ,
,
在Rt△BEM中,∠BME=90°,∠BEM=∠A=30°
∴BM= ![]() BE=1+
BE=1+ ![]() .
.
【解析】(1)延长FC至H,由AB是⊙O的直径,得出∠ACB=90°,由EM⊥AB,得出∠EMB=∠ACB=90°,证得△ABC∽△EMB,得出∠CEF=∠CAB,由弦切角定理得出∠CAB=∠BCH,由对顶角相等得出∠BCH=∠ECF,推出∠CEF=∠ECF,即可得出结论;(2)利用含30度的直角三角形三边的性质得出BC= ![]() AB=2,AC=
AB=2,AC= ![]() BC=2
BC=2 ![]() ,则CE=2
,则CE=2 ![]() ,所以BE=BC+CE=2+2
,所以BE=BC+CE=2+2 ![]() ,然后在Rt△BEM中计算出BM=
,然后在Rt△BEM中计算出BM= ![]() BE即可.
BE即可.
【考点精析】本题主要考查了三角形的外接圆与外心和切线的性质定理的相关知识点,需要掌握过三角形的三个顶点的圆叫做三角形的外接圆,其圆心叫做三角形的外心;切线的性质:1、经过切点垂直于这条半径的直线是圆的切线2、经过切点垂直于切线的直线必经过圆心3、圆的切线垂直于经过切点的半径才能正确解答此题.


 导学全程练创优训练系列答案
导学全程练创优训练系列答案科目:初中数学 来源: 题型:
【题目】如图1:在四边形ABCD中,AB=AD,∠BAD=120°,∠B=∠ADC=90°.E、F分别是BC、CD上的点.且∠EAF=60°.探究图中线段BE、EF、FD之间的数量关系.
小王同学探究此问题的方法是,延长FD到点G,使DG=BE.连结AG,先证明△ABE≌△ADG,再证明△AEF≌△AGF,可得出结论,他的结论应是 ;

探索延伸:
如图2,若在四边形ABCD中,AB=AD,∠B+∠D=180°.E、F分别是BC、CD上的点,且∠EAF=![]() ∠BAD,上述结论是否仍然成立,并说明理由;
∠BAD,上述结论是否仍然成立,并说明理由;
实际应用:
如图3,在某次军事演习中,舰艇甲在指挥中心(O处)北偏西30°的A处,舰艇乙在指挥中心南偏东70°的B处,并且两舰艇到指挥中心的距离相等,接到行动指令后,舰艇甲向正东方向以60海里/小时的速度前进,舰艇乙沿北偏东50°的方向以80海里/小时的速度前进1.5小时后,指挥中心观测到甲、乙两舰艇分别到达E,F处,且两舰艇之间的夹角为70°,试求此时两舰艇之间的距离?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将油箱注满k升油后,轿车行驶的总路程S(单位:千米)与平均耗油量a(单位:升/千米)之间是反比例函数关系S= ![]() (k是常数,k≠0).已知某轿车油箱注满油后,以平均耗油量为每千米耗油0.1升的速度行驶,可行驶760千米,当平均耗油量为0.08升/千米时,该轿车可以行驶千米.
(k是常数,k≠0).已知某轿车油箱注满油后,以平均耗油量为每千米耗油0.1升的速度行驶,可行驶760千米,当平均耗油量为0.08升/千米时,该轿车可以行驶千米.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数y=ax2+bx+c(a≠0)的部分图象如图,图象过点(﹣1,0),对称轴为直线x=2,下列结论:
①4a+b=0;
②9a+c<3b;
③25a+5b+c=0;
④当x>2时,y随x的增大而减小.
其中正确的结论有( )
A.1个
B.2个
C.3个
D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一个暗箱中装有红、黄、白三种颜色的乒乓球(除颜色外其余均相同),其中白球、黄球各1个,且从中随机摸出一个球是白球的概率是 ![]() .
.
(1)求暗箱中红球的个数;
(2)先从暗箱中随机摸出一个球,记下颜色放回,再从暗箱中随机摸出一个球,求两次摸到的球颜色不同的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在边长为100米的正三角形花坛的边上,甲、乙两人分别从两个顶点同时出发,按逆时针方向行走,已知甲的速度是42米/分,乙的速度是34米/分.出发后________分钟,甲乙两人第一次走在同一条边上.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知在平面直角坐标系中有三点A(﹣2,1)、B(3,1)、C(2,3).请回答如下问题:

(1)在坐标系内描出点A、B、C的位置,并求△ABC的面积
(2)在平面直角坐标系中画出△A′B′C′,使它与△ABC关于x轴对称,并写出△A′B′C′三顶点的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB∥DE,AC∥DF,AC=DF,要使△ABC≌△DEF需再补充一个条件,下列条件中,不能选择的是( )
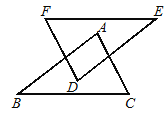
A. AB=DE B. BC=EF C. EF∥BC D. ∠B=∠E
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了倡导“节约用水,从我做起”的活动,某市政府决定对市直机关500户家庭的用水情况作一次调查,调查小组随机抽查了其中100户家庭一年的月平均用水量(单位:吨).并将调查结果制成了如图所示的条形统计图.
(1)求这100个样本数据的平均数、众数和中位数;
(2)根据样本数据,估计该市直机关500户家庭中月平均用水量不超过12吨的约有多少户?

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com