
分析 (1)根据二次根式的乘除法则运算;
(2)先计算单项式乘多项式,然后把中括号内合并后进行多项式除单项式的运算.
解答 解:(1)原式=-$\frac{1}{4}$×8×12×$\sqrt{\frac{2}{75}×\frac{5}{8}×\frac{5}{2}}$
=-2$\sqrt{6}$;
(2)原式=(4xy+8xy2-8xy2-2x2y)÷(-2x)
=(4xy-2x2y)÷(-2x)
=-2y+xy.
点评 本题考查了二次根式的计原式=算:先把各二次根式化为最简二次根式,再进行二次根式的乘除运算,然后合并同类二次根式.在二次根式的混合运算中,如能结合题目特点,灵活运用二次根式的性质,选择恰当的解题途径,往往能事半功倍.也考查了整式的混合运算.


 名校联盟快乐课堂系列答案
名校联盟快乐课堂系列答案 黄冈创优卷系列答案
黄冈创优卷系列答案科目:初中数学 来源: 题型:解答题
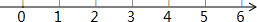 解不等式组$\left\{\begin{array}{l}{x+3≥4①}\\{3x-4≤11②}\end{array}\right.$
解不等式组$\left\{\begin{array}{l}{x+3≥4①}\\{3x-4≤11②}\end{array}\right.$查看答案和解析>>
科目:初中数学 来源: 题型:填空题
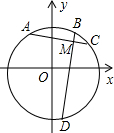 半径为2的圆的圆心O在直角坐标系的原点,两条互相垂直的弦AC和BD相交于点M(1,$\sqrt{2}$),则四边形ABCD的面积的最大值与最小值的差是1.
半径为2的圆的圆心O在直角坐标系的原点,两条互相垂直的弦AC和BD相交于点M(1,$\sqrt{2}$),则四边形ABCD的面积的最大值与最小值的差是1.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
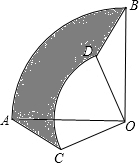 把两个圆心角是90°的扇形OAB与OCD如图那样叠放在一起,连接AC、BD.
把两个圆心角是90°的扇形OAB与OCD如图那样叠放在一起,连接AC、BD.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com