
【题目】已知△ABC是等边三角形,P为△ABC所在平面内一个动点,BP=BA,若0°﹤∠PBC﹤ 180°,且∠PBC的平分线上一点D满足DB=DA.
(1)当BP和BA重合时(如图1),则∠BPD=______°.
(2)当BP在∠ABC内部时(如图2),求∠BPD的度数
(3)当BP在∠ABC外部时,请直接写出∠BPD的度数,并画出相应的图形.


【答案】(1)30;(2)∠BPD=30°;(3)图形见解析,∠BPD=30°或150°.
【解析】
(1)由于P,A重合,DP=DB,∠DBP=∠DPB,因为DB是∠PBC的平分线,因此,∠DBP=∠DPB=30°;
(2)本题可通过构建全等三角形来求解.连接CD,BP=BC,BD又是∠PBC的平分线,三角形PBD和三角形CBD中又有一公共边,因此两三角形全等,∠BPD=∠BCD,那么关键是求∠BCD的值,那么我们就要看∠BCD和∠ACB的关系了,可通过证明三角形ACD和BCD全等来得出,这两个三角形中,BD=AD,BC=AC,有一条公共边CD因此∠BCD=∠ACD=30°,那么就求出∠BPD的度数了;
(3)同(2)的证法完全一样,步骤有2个,一是得出∠BCD的度数,二是证明三角形BPD和BCD全等,同(2)完全一样.
(当∠BPD是钝角时,∠BPD=∠BCD=(360-60)÷2=150°,还是用的(2)中的三角形BPD,BCD全等,BCD,ACD全等)
解:(1)30°
(2)连结CD
∵ D在∠PBC的平分线上
∴∠PBD=∠CBD
∵△ABC是等边三角形
∴BA=BC=AC,∠ACB=60°
∵BP=BA
∴BP=BC
∵BD=BD
∴△PBD≌△CBD(SAS)
∴∠BPD=∠BCD
∵DB=DA,BC=AC,CD=CD
∴△BCD≌△ACD
∴∠BCD=∠ACD=![]() ∠ACB=30°
∠ACB=30°
∴∠BPD=30°

(3)∠BPD=30°或150°





 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】小明同学想测量位于池塘两端的A、B两点的距离.他沿着与直线AB平行的道路EF行走,当行走到点C处,测得∠ACF=45°,再向前行走一段距离时到点D处,侧得∠BDF=65°.若直线AB与EF之间的距离为60米.
(1)设池塘两端的距离AB=x米,试用含x的代数式表示CD的长;
(2)当CD=100米时,求A、B两点的距离(计算结果精确到个位).(参考数据:sin45°≈0.71,cos65°≈0.42,tan65°≈2.14.)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,AB=AC,点D是直线BC上一点(不与B、C重合),以AD为一边在AD的右侧作△ADE,使AD=AE,∠DAE =∠BAC,连接CE.
(1)如图1,当点D在线段BC上,如果∠BAC=90°,则∠BCE=________度;
(2)设![]() ,
,![]() .
.
①如图2,当点在线段BC上移动,则![]() ,
,![]() 之间有怎样的数量关系?请说明理由;
之间有怎样的数量关系?请说明理由;
②当点在直线BC上移动,则![]() ,
,![]() 之间有怎样的数量关系?请直接写出你的结论.
之间有怎样的数量关系?请直接写出你的结论.




查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市长途客运站每天6:30—7:30开往某县的三辆班车票价相同,但车的舒适程度不同.小张和小王因事需在这一时段乘车去该县,但不知道三辆车开来的顺序,两人采用不同的乘车方案:小张无论如何决定乘坐开来的第一辆车,而小王则是先观察后上车,当第一辆车开来时,他不上车,而是仔细观察车的舒适状况.若第二辆车的状况比第一辆车好,他就上第二辆车;若第二辆车不如第一辆车,他就上第三辆车.若按这三辆车的舒适程度分为优、中、差三等,请你思考并回答下列问题:
(1)三辆车按出现的先后顺序共有哪几种可能?
(2)请列表分析哪种方案乘坐优等车的可能性大?为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,点D为BC边上一点,∠1=∠2=∠3,AC=AE.
求证:△ABC≌△ADE;(填空)
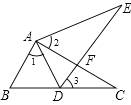
证明:∵∠2+∠E+∠AFE=180° ( )
∠3+∠C+∠CFD=180°(同理)
又∵∠2=∠3( )
∠AFE=∠CFD( )
∴∠E=_________.
∵∠1=∠2(已知)
∴∠1+∠CAD=∠2+∠_______.
即∠BAC=∠DAE
在△ABC和△ADE中
∴△ABC≌△ADE( ).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场销售一种商品,进价为每个20元,规定每个商品售价不低于进价,且不高于60元.经调查发 现,每天的销售量y(个)与每个商品的售价x(元)满足一次函数关系,其部分数据如下表所示:

(1)求y与x之间的函数关系式;
(2)设商场每天获得的总利润为w(元),求w与x之间的函数关系式;
(3)不考虑其他因素,当商品的售价为多少元时,商场每天获得的总利润最大,最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】 P为等边△ABC的边AB上一点,Q为BC延长线上一点,且PA=CQ,连PQ交AC边于D.
(1)证明:PD=DQ.
(2)如图2,过P作PE⊥AC于E,若AB=6,求DE的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,平面直角坐标系中,△ABC为等边三角形,其中点A,B,C的坐标分别为(-3,-1),(-3,-3),(-3+![]() ,-2).现以y轴为对称轴作△ABC的对称图形,得△A1B1C1,再以x轴为对称轴作△A1B1C1的对称图形,得△A2B2C2.
,-2).现以y轴为对称轴作△ABC的对称图形,得△A1B1C1,再以x轴为对称轴作△A1B1C1的对称图形,得△A2B2C2.
(1)直接写出点C1,C2的坐标.
(2)能否通过一次旋转将△ABC旋转到△A2B2C2的位置?若能,请直接写出所旋转的度数;若不能,请说明理由.
(3)设当△ABC的位置发生变化时,△A2B2C2,△A1B1C1与△ABC之间的对称关系始终保持不变.
①当△ABC向上平移多少个单位长度时,△A1B1C1与△A2B2C2完全重合?并直接写出此时点C的坐标;
②将△ABC绕点A顺时针旋转α°(0≤α≤180),使△A1B1C1与△A2B2C2完全重合,此时α的值为多少?点C的坐标又是什么?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形网格中的每个小正方形的边长都是1,每个小格的顶点叫做格点.
(1)在图1中以格点为顶点画一个面积为10的正方形;
(2)在图2中以格点为顶点画一个三角形,使三角形三边长分别为2、![]() 、
、![]() ;
;
(3)如图3,点A、B、C是小正方形的顶点,求∠ABC的度数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com