Question

【题目】 P为等边△ABC的边AB上一点，Q为BC延长线上一点，且PA＝CQ，连PQ交AC边于D．

（1）证明：PD＝DQ．

（2）如图2，过P作PE⊥AC于E，若AB＝6，求DE的长．

Answer 1

【答案】（1）证明见解析；（2）DE＝3．

【解析】

（1）过点P作PF∥BC交AC于点F；证出△APF也是等边三角形，得出AP=PF=AF=CQ，由AAS证明△PDF≌△QDC，得出对应边相等即可；

（2）过P作PF∥BC交AC于F．同（1）由AAS证明△PFD≌△QCD，得出对应边相等FD=CD，证出AE+CD=DEAC，即可得出结果．

（1）如图1所示，点P作PF∥BC交AC于点F．

∵△ABC是等边三角形，

∴△APF也是等边三角形，AP=PF=AF=CQ．

∵PF∥BC，∴∠PFD=∠DCQ．

在△PDF和△QDC中，，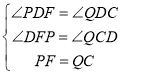

∴△PDF≌△QDC（AAS），

∴PD=DQ；

（2）如图2所示，过P作PF∥BC交AC于F．

∵PF∥BC，△ABC是等边三角形，

∴∠PFD=∠QCD，△APF是等边三角形，

∴AP=PF=AF．

∵PE⊥AC，∴AE=EF．

∵AP=PF，AP=CQ，∴PF=CQ．

在△PFD和△QCD中，，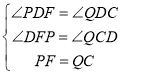

∴△PFD≌△QCD（AAS），

∴FD=CD．

∵AE=EF，∴EF+FD=AE+CD，

∴AE+CD=DEAC．

∵AC=6，∴DE=3．