
【题目】某电视台的娱乐节目《周末大放送》有这样的翻奖牌游戏:如图所示,将一个正方形均分成9等份,数字的背面写有祝福语或奖金数.游戏规则是:每次翻动正面一个数字,看看反面对应的内容,就可知是得奖还是得到温馨祝福.
正面:
1 | 2 | 3 |
4 | 5 | 6 |
7 | 8 | 9 |
反面:
祝你开心 | 万事如意 | 奖金1 000元 |
身体健康 | 心想事成 | 奖金500元 |
奖金100元 | 生活愉快 | 谢谢参与 |
请你完成下列问题:
(1)翻到奖金1 000元的概率是多少?
(2)翻不到奖金的概率是多少?
(3)一选手准备在奇数中选择一个数字,他获得奖金的概率是多少?
【答案】(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]()
【解析】
(1)用“翻到奖金1000元”的数字牌数除以总的牌数,即可求出“翻到奖金1000元”的概率;
(2)用“翻不到奖金”的数字牌数除以总的牌数,即可求出“翻不到奖金”的概率;
(3)用“奇数有奖金”的数字个数除以奇数的个数,即可求出“奇数中选择一个数字,获得奖金”的概率.
(1)根据题意可得:有参加游戏的人可随意翻动一个数字牌,共9种情况;
其中有1个是“翻到奖金1000元”,
所以“翻到奖金1000元”的概率是![]() ;
;
(2)根据题意可得:有参加游戏的人可随意翻动一个数字牌,共9种情况,
其中有6个是“翻不到奖金”,
所以“翻不到奖金”的概率![]() =
=![]() ;
;
(3)因为9个数中共有1,3,5,7,9共5个奇数,其中有奖金的共2个,故他获得奖金的概率是![]() .
.


 新题型全程检测期末冲刺100分系列答案
新题型全程检测期末冲刺100分系列答案科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=BC,∠ABC=30°,BD平分∠ABC交AC于点D,BC的垂直平分线EF交BC于点E,交BD于点F,若BF=6,则AC的长为____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,以BC为直径的⊙O交AC于点E,过点E作AB的垂线交AB于点F,交CB的延长线于点G,且∠ABG=2∠C.
(1)求证:EG是⊙O的切线;
(2)若tanC=![]() ,AC=8,求⊙O的半径.
,AC=8,求⊙O的半径.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,AB=AC,点D是直线BC上一点(不与B、C重合),以AD为一边在AD的右侧作△ADE,使AD=AE,∠DAE =∠BAC,连接CE.
(1)如图1,当点D在线段BC上,如果∠BAC=90°,则∠BCE=________度;
(2)设![]() ,
,![]() .
.
①如图2,当点在线段BC上移动,则![]() ,
,![]() 之间有怎样的数量关系?请说明理由;
之间有怎样的数量关系?请说明理由;
②当点在直线BC上移动,则![]() ,
,![]() 之间有怎样的数量关系?请直接写出你的结论.
之间有怎样的数量关系?请直接写出你的结论.




查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在直角坐标系中,先描出点![]() ,点
,点![]() .
.

(1)描出点![]() 关于
关于![]() 轴的对称点
轴的对称点![]() 的位置,写出
的位置,写出![]() 的坐标 ;
的坐标 ;
(2)用尺规在![]() 轴上找一点
轴上找一点![]() ,使
,使![]() 的值最小(保留作图痕迹);
的值最小(保留作图痕迹);
(3)用尺规在![]() 轴上找一点
轴上找一点![]() ,使
,使![]() (保留作图痕迹).
(保留作图痕迹).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市长途客运站每天6:30—7:30开往某县的三辆班车票价相同,但车的舒适程度不同.小张和小王因事需在这一时段乘车去该县,但不知道三辆车开来的顺序,两人采用不同的乘车方案:小张无论如何决定乘坐开来的第一辆车,而小王则是先观察后上车,当第一辆车开来时,他不上车,而是仔细观察车的舒适状况.若第二辆车的状况比第一辆车好,他就上第二辆车;若第二辆车不如第一辆车,他就上第三辆车.若按这三辆车的舒适程度分为优、中、差三等,请你思考并回答下列问题:
(1)三辆车按出现的先后顺序共有哪几种可能?
(2)请列表分析哪种方案乘坐优等车的可能性大?为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
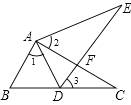
【题目】如图,在△ABC中,点D为BC边上一点,∠1=∠2=∠3,AC=AE.
求证:△ABC≌△ADE;(填空)
证明:∵∠2+∠E+∠AFE=180° ( )
∠3+∠C+∠CFD=180°(同理)
又∵∠2=∠3( )
∠AFE=∠CFD( )
∴∠E=_________.
∵∠1=∠2(已知)
∴∠1+∠CAD=∠2+∠_______.
即∠BAC=∠DAE
在△ABC和△ADE中
∴△ABC≌△ADE( ).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】 P为等边△ABC的边AB上一点,Q为BC延长线上一点,且PA=CQ,连PQ交AC边于D.
(1)证明:PD=DQ.
(2)如图2,过P作PE⊥AC于E,若AB=6,求DE的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某省为推广新能源汽车,计划连续五年给予财政补贴.补贴开始时间为![]() 年度,截止时间为
年度,截止时间为![]() 年度.补贴期间后一年度的补贴额均在前一年度补贴额基础上递增.计划前三年,每年度按固定额度
年度.补贴期间后一年度的补贴额均在前一年度补贴额基础上递增.计划前三年,每年度按固定额度![]() 亿元递增;后两年均在上一年的基础上按相同增长率递增.已知
亿元递增;后两年均在上一年的基础上按相同增长率递增.已知![]() 年度计划补贴额为
年度计划补贴额为![]() 亿元.
亿元.
![]() 若
若![]() 年度计划补贴额比
年度计划补贴额比![]() 年度至少增加
年度至少增加![]() ,求
,求![]() 的取值范围;
的取值范围;
![]() 若预计
若预计![]() 这五年补贴总额比
这五年补贴总额比![]() 年度补贴额的
年度补贴额的![]() 倍还多
倍还多![]() 亿元,求后两年财政补贴的增长率.
亿元,求后两年财政补贴的增长率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com