练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

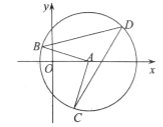
    【题目】如图，点、在上，点在轴的正半轴上，点是上第一象限内的一点，若，则圆心的坐标为__．

    【答案】

    【解析】

    分别过点B，C作x轴的垂线，垂足分别为E，F，先通过圆周角定理可得出∠BAC=90°，再证明△BEA≌△AFC，得出AE=CF=4，再根据AO=AE-OE可得出结果．

    解：分别过点B，C作x轴的垂线，垂足分别为E，F，

    ∵∠D=45°，∴∠BAC=90°．

    ∴∠BAE+∠ABE=90°，∠BAE+∠CAF=90°，

    ∴∠ABE=∠CAF，

    又AB=AC，∠AEB=∠AFC=90°，

    ∴△BEA≌△AFC（AAS），

    ∴AE=CF，

    又∵B，C的坐标为、，

    ∴OE=1，CF=4，

    ∴OA=AE-OE=CF-OE=3．

    ∴点A的坐标为（3，0）．

    故答案为：（3，0）．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】为了扎实推进精准扶贫工作，某地出台了民生兜底、医保脱贫、教育救助、产业扶持、养老托管和易地搬迁这六种帮扶措施，每户贫困户都享受了2到5种帮扶措施，现把享受了2种、3种、4种和5种帮扶措施的贫困户分别称为A、B、C、D类贫困户．为检査帮扶措施是否落实，随机抽取了若干贫困户进行调查，现将收集的数据绘制成下面两幅不完整的统计图：

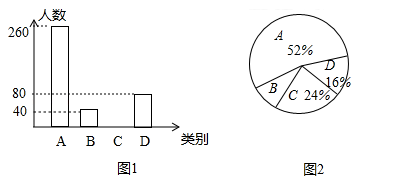
    请根据图中信息回答下面的问题：

    （1）本次抽样调查了多少户贫困户？

    （2）抽查了多少户C类贫困户？并补全统计图；

    （3）若该地共有13000户贫困户，请估计至少得到4项帮扶措施的大约有多少户？

    （4）为更好地做好精准扶贫工作，现准备从D类贫困户中的甲、乙、丙、丁四户中随机选取两户进行重点帮扶，请用树状图或列表法求出恰好选中甲和丁的概率．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某射击运动员练习射击，5次成绩分别是：8、9、7、8、x（单位：环）．下列说法中正确的是（　　）

    A. 若这5次成绩的中位数为8，则x＝8

    B. 若这5次成绩的众数是8，则x＝8

    C. 若这5次成绩的方差为8，则x＝8

    D. 若这5次成绩的平均成绩是8，则x＝8

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】在平面直角坐标系中，点O（0，0），点A（﹣3，0）．已知抛物线y＝﹣x2+2mx+3（m为常数），顶点为P．

    （1）当抛物线经过点A时，顶点P的坐标为　 　；

    （2）在（1）的条件下，此抛物线与x轴的另一个交点为点B，与y轴交于点C．点Q为直线AC上方抛物线上一动点．

    ①如图1，连接QA、QC，求△QAC的面积最大值；

    ②如图2，若∠CBQ＝45°，请求出此时点Q坐标．

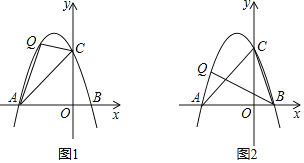
    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】空间任意选定一点，以点为端点作三条互相垂直的射线，，．这三条互相垂直的射线分别称作轴、轴、轴，统称为坐标轴，它们的方向分别为（水平向前），（水平向右），（竖直向上）方向，这样的坐标系称为空间直角坐标系．将相邻三个面的面积记为，且的小长方体称为单位长方体，现将若干个单位长方体在空间直角坐标系内进行码放，要求码放时将单位长方体所在的面与轴垂直，所在的面与轴垂直，所在的面与轴垂直，如图所示．若将轴方向表示的量称为几何体码放的排数，轴方向表示的量称为几何体码放的列数，轴方向表示的量称为几何体码放的层数；如图是由若干个单位长方体在空间直角坐标内码放的一个几何体，其中这个几何体共码放了排列层，用有序数组记作 (1，2，6)，如图的几何体码放了排列层，用有序数组记作 (2，3，4)．这样我们就可用每一个有序数组表示一种几何体的码放方式．

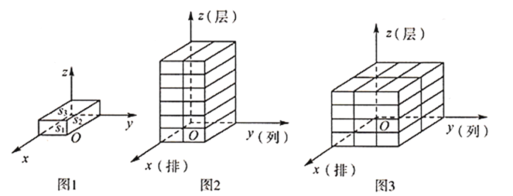
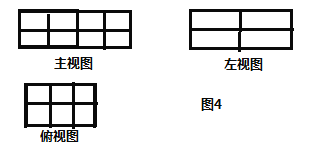
    （1）有序数组 (3，2，4)所对应的码放的几何体是_____；

    （2）图是由若干个单位长方体码放的一个几何体的三视图，则这种码放方式的有序数组为(___，____，____)，组成这个几何体的单位长方体的个数为____个；

    （3）为了进一步探究有序数组的几何体的表面积公式，某同学针对若干个单位长方体进行码放，制作了下列表格：

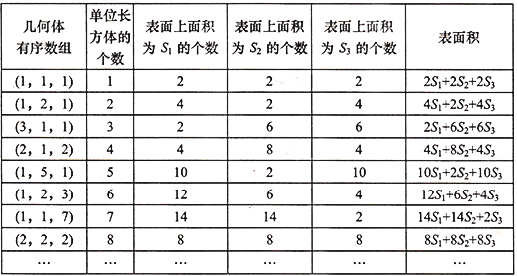
    根据以上规律，请直接写出有序数组的几何体表面积的计算公式；（用表示）

    （4）当时，对由个单位长方体码放的几何体进行打包，为了节约外包装材料，我们可以对个单位长方体码放的几何体表面积最小的规律进行探究，请你根据自己探究的结果直接写出使几何体表面积最小的有序数组，这个有序数组为(___，___，___)，此时求出的这个几何体表面积的大小为________．（缝隙不计）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图1，小明用一张边长为的正方形硬纸板设计一个无盖的长方体纸盒，从四个角各剪去一个边长为的正方形，再折成如图2所示的无盖纸盒，记它的容积为．

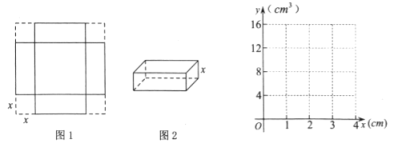
    （1）关于的函数表达式是__________，自变量的取值范围是___________．

    （2）为探究随的变化规律，小明类比二次函数进行了如下探究：

    ①列表：请你补充表格中的数据：

    0

    0．5

    1

    1．5

    2

    2．5

    3

    0

    12．5

    13．5

    2．5

    0

    ②描点：把上表中各组对应值作为点的坐标，在平面直角坐标系中描出相应的点；

    ③连线：用光滑的曲线顺次连结各点．

    （3）利用函数图象解决：若该纸盒的容积超过，估计正方形边长的取值范围．（保留一位小数）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

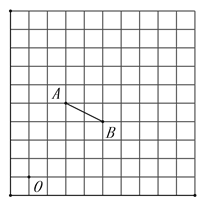
    【题目】如图，在由边长为1个单位长度的小正方形组成的10×10网格中，已知点O，A，B均为网格线的交点.

    （1）在给定的网格中，以点O为位似中心，将线段AB放大为原来的2倍，得到线段（点A，B的对应点分别为）.画出线段;

    （2）将线段绕点逆时针旋转90°得到线段.画出线段;

    （3）以为顶点的四边形的面积是 个平方单位.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

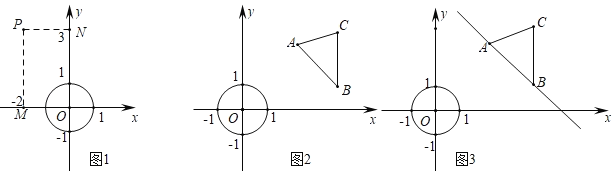
    【题目】在平面直角坐标系xOy，对于点P（xp，yp）和图形G，设Q（xQ，yQ）是图形G上任意一点，|xp﹣xQ|的最小值叫点P和图形G的“水平距离”，|yp﹣yQ|的最小值叫点P和图形G的“竖直距离”，点P和图形G的“水平距离”与“竖直距离”的最大值叫做点P和图形G的“绝对距离”

    例如：点P（﹣2，3）和半径为1的⊙O，因为⊙O上任一点Q（xQ，yQ）满足﹣1≤xQ≤1，﹣1≤yQ≤1，点P和⊙O的“水平距离”为|﹣2﹣xQ|的最小值，即|﹣2﹣（﹣1）|=1，点P和⊙O的“竖直距离”为|3﹣yQ|的最小值即|3﹣1|=2，因为2＞1，所以点P和⊙O的“绝对距离”为2．

    已知⊙O半径为1，A（2，），B（4，1），C（4，3）

    （1）①直接写出点A和⊙O的“绝对距离”

    ②已知D是△ABC边上一个动点，当点D与⊙O的“绝对距离”为2时，写出一个满足条件的点D的坐标；

    （2）已知E是△ABC边一个动点，直接写出点E与⊙O的“绝对距离”的最小值及相应的点E的坐标

    （3）已知P是⊙O上一个动点，△ABC沿直线AB平移过程中，直接写出点P与△ABC的“绝对距离”的最小值及相应的点P和点C的坐标．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，P是边长为3的等边△ABC边AB上一动点，沿过点P的直线折叠∠B，使点B落在AC上，对应点为D，折痕交BC于E，点D是AC的一个三等分点，PB的长为______.

    查看答案和解析>>

    同步练习册答案