
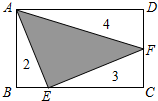
 如图,矩形ABCD被分成四部分,其中△ABE、△ECF、△ADF的面积分别为2、3、4,则△AEF的面积为7.
如图,矩形ABCD被分成四部分,其中△ABE、△ECF、△ADF的面积分别为2、3、4,则△AEF的面积为7. 分析 首先设AB=a,BC=b,由△CEF,△ABE,△ADF的面积分别是2,3,4可得S△ABE=$\frac{1}{2}$×a×BE=2,S△CEF=$\frac{1}{2}$×EC×FC=3,则可得S△ADF=$\frac{1}{2}$×(a-$\frac{6ab}{ab-4}$)×b=4,继而求得ab的值.
解答 解:设AB=a,BC=b,
∵△CEF,△ABE,△ADF的面积分别是2,3,4,
∴S△ABE=$\frac{1}{2}$×a×BE=2,
∴BE=$\frac{4}{a}$,
∴EC=BC-BE=b-$\frac{4}{a}$,
∵S△CEF=$\frac{1}{2}$×EC×FC=3,
∴FC=$\frac{6a}{ab-4}$,
∴DF=CD-CF=a-$\frac{6a}{ab-4}$,
∴S△ADF=$\frac{1}{2}$×(a-$\frac{6a}{ab-4}$)×b=4,
∴(ab)2-18ab+32=0,
解得:ab=16或ab=2(不合题意,舍去),
∴S△AEF=16-3-4-2=7,
故答案为:7.
点评 此题考查了面积与等积变换的知识以及直角三角形与矩形的性质.此题难度适中,注意掌握方程思想与数形结合思想的应用.


科目:初中数学 来源: 题型:填空题


查看答案和解析>>
科目:初中数学 来源: 题型:解答题
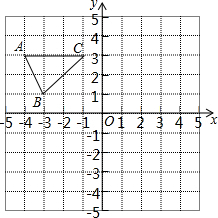 如图,已知△ABC的三个顶点坐标分别为A(-4,3),B(-3,1),C(-1,3).
如图,已知△ABC的三个顶点坐标分别为A(-4,3),B(-3,1),C(-1,3).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
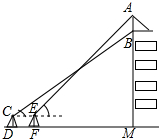 为了弘扬九十五中学办学理念,我校将“立己立人,尽善尽美”的校训印在旗帜上,放置在教学楼的顶部(如图所示).小华在教学楼前空地上的点D处,用1米高的测角仪CD,从点C测得旗帜的底部B的仰角为37°,然后向教学楼正方向走了4.8米到达点F处,又从点E测得旗帜的顶部A的仰角为45°.若教学楼高BM=19米,且点A、B、M在同一直线上,求旗帜AB的高度(参考数据:sin37°≈0.60,cos37°≈0.81,tan37°≈0.75.
为了弘扬九十五中学办学理念,我校将“立己立人,尽善尽美”的校训印在旗帜上,放置在教学楼的顶部(如图所示).小华在教学楼前空地上的点D处,用1米高的测角仪CD,从点C测得旗帜的底部B的仰角为37°,然后向教学楼正方向走了4.8米到达点F处,又从点E测得旗帜的顶部A的仰角为45°.若教学楼高BM=19米,且点A、B、M在同一直线上,求旗帜AB的高度(参考数据:sin37°≈0.60,cos37°≈0.81,tan37°≈0.75.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com