
 如图,在Rt△ABC中,∠C=90°,BC=6cm,AC=8cm,按图中所示方法将△BCD沿BD折叠,使点C落在AB边的C′点.
如图,在Rt△ABC中,∠C=90°,BC=6cm,AC=8cm,按图中所示方法将△BCD沿BD折叠,使点C落在AB边的C′点.分析 (1)利用勾股定理列式求出AB,根据翻折变换的性质可得BC′=BC,C′D=CD,然后求出AC′,设CD=x,表示出C′D、AD,然后利用勾股定理列方程求解即可;
(2)根据三角形的面积公式计算即可.
解答 解:(1)∵∠C=90°,BC=6cm,AC=8cm,
∴AB=$\sqrt{B{C}^{2}+A{C}^{2}}$=10cm,
由翻折变换的性质得,BC′=BC=6cm,C′D=CD,
∴AC′=AB-BC′=10-6=4cm,
设CD=x,则C′D=x,AD=8-x,
在Rt△AC′D中,由勾股定理得,AC′2+C′D2=AD2,
即42+x2=(8-x)2,
解得x=3,
即CD=3cm.
(2)∵∠AC′D=90°,
∴△ADC′的面积=$\frac{1}{2}$×AC′×C′D=$\frac{1}{2}$×4×3=6(cm2).
点评 本题考查了翻折变换的性质,勾股定理,此类题目熟记性质并利用勾股定理列出方程是解题的关键.


 文敬图书课时先锋系列答案
文敬图书课时先锋系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
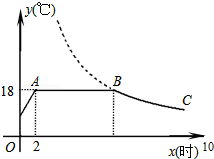 我市某蔬菜生产基地在气温较低时,用装有恒温系统的大棚栽培一种在自然光照且温度为18℃的条件下生长最快的新品种.下图是某天恒温系统从开启到关闭及关闭后,大棚内温度y(℃)随时间x(小时)变化的函数图象,其中BC段是双曲线y=$\frac{k}{x}$的一部分.请根据图中信息解答下列问题:
我市某蔬菜生产基地在气温较低时,用装有恒温系统的大棚栽培一种在自然光照且温度为18℃的条件下生长最快的新品种.下图是某天恒温系统从开启到关闭及关闭后,大棚内温度y(℃)随时间x(小时)变化的函数图象,其中BC段是双曲线y=$\frac{k}{x}$的一部分.请根据图中信息解答下列问题:查看答案和解析>>
科目:初中数学 来源: 题型:选择题
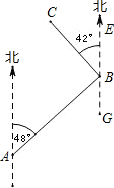 如图,在A、B两处之间要修一条笔直的公路,从A地测得公路走向是北偏东48°,A、B两地同时开工,若干天后公路准确接通.若公路AB长10千米另一条公路BC长7千米,且BC的走向是北偏西42°,则A到公路BC的距离为( )
如图,在A、B两处之间要修一条笔直的公路,从A地测得公路走向是北偏东48°,A、B两地同时开工,若干天后公路准确接通.若公路AB长10千米另一条公路BC长7千米,且BC的走向是北偏西42°,则A到公路BC的距离为( )| A. | 3 | B. | 7 | C. | 10 | D. | 无法确定 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
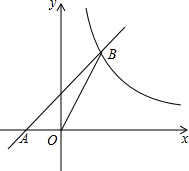 如图,直线y=kx+2k (k≠0)与x轴交于点A,与反比例函数y=(m+3)x2m-1在第一象限内的图象交于点B,已知S△AOB=3.
如图,直线y=kx+2k (k≠0)与x轴交于点A,与反比例函数y=(m+3)x2m-1在第一象限内的图象交于点B,已知S△AOB=3.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
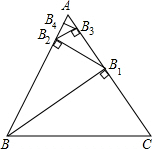 如图,△ABC是一个边长为1的等边三角形,BB1是△ABC的高,B1B2是△ABB1的高,B2B3是△AB1B2的高,…,Bn-1Bn是△ABn-2Bn-1的高,则Bn-1Bn的长是$\frac{\sqrt{3}}{{2}^{n}}$.
如图,△ABC是一个边长为1的等边三角形,BB1是△ABC的高,B1B2是△ABB1的高,B2B3是△AB1B2的高,…,Bn-1Bn是△ABn-2Bn-1的高,则Bn-1Bn的长是$\frac{\sqrt{3}}{{2}^{n}}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
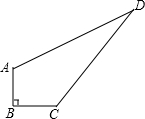 老张家有一块草坪如图所示.家里想整理它,需要知道其面积.老张测量了草坪各边得知:AB=3米,BC=4米,AD=12米,CD=13米,且AB⊥CB.请你帮老张家计算一下这块草坪的面积.
老张家有一块草坪如图所示.家里想整理它,需要知道其面积.老张测量了草坪各边得知:AB=3米,BC=4米,AD=12米,CD=13米,且AB⊥CB.请你帮老张家计算一下这块草坪的面积.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com