
分析 (1)作AD⊥OB于点D,在直角△ABD中利用勾股定理即可求解;
(2)根据三角形的外角的性质即可证得∠MAN=∠AOM=45°,作∠NAE=∠NAM=45°,使点E与M在AN两侧,截取AE=AM,连接BE,NE,作AH垂直MN于H.证明△BAE≌△OAM,在直角△AHN中,利用勾股定理即可求解;
(3)连接PM,作MK垂直PN于K,根据三角形的面积公式即可证得$\frac{PN}{PO}=\frac{NM}{OM}$,设PN=t,利用t表示PN和PO,据此即可列方程求解.
解答 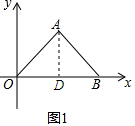 解:(1)作AD⊥OB于点D.
解:(1)作AD⊥OB于点D.
则D的坐标是(6,0),则AD=6,BD=6,
则AB=$\sqrt{A{D}^{2}+B{D}^{2}}$=$\sqrt{{6}^{2}+{6}^{2}}$=6$\sqrt{2}$;
(2)∵∠AMN=∠AON+∠OAM,∠OAN=∠OAM+∠MAN,
又∵∠AMN=∠OAN,
∴∠MAN=∠AOM=45°,
∵点A为(6,6),点B为(12,0),
∴AO=AB,∠OAB=90°.
作∠NAE=∠NAM=45°,使点E与M在AN两侧,截取AE=AM,连接BE,NE;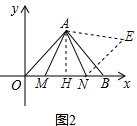
作AH垂直MN于H.
∵∠MAE=∠OAB=90°.
∴∠BAE=∠OAM;
在△BAE和△OAM中,
$\left\{\begin{array}{l}{AE=AM}\\{∠BAE=∠OAM}\\{AB=AO}\end{array}\right.$,
∴△BAE≌△OAM,
∴BE=OM=3;
NE=MN;∠ABE=∠AOM=45°,则∠NBE=90°.
设BN=x,则NE=MN=OB=OM-BN=9-x.
BN2+BE2=NE2,即x2+9=(9-x)2,
x=4,ON=8,HN=ON-OH=8-6=2,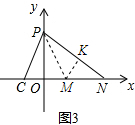
故AN=$\sqrt{A{H}^{2}+H{N}^{2}}$=2$\sqrt{10}$,
(3)连接PM.OM=OC=3,PO垂直平分CM,则PC=PM,∠MPO=∠CPO;
若∠NPO=2∠CPO,则∠NPO=2∠MPO,即∠NPM=∠MPO.
作MK垂直PN于K,则MK=MO=3.
故$\frac{{S}_{△NPM}}{{S}_{△MPO}}=\frac{PN}{PO}$(等高三角形的面积比等于底之比);
又∵$\frac{{S}_{γ△NPM}}{{S}_{△PMO}}=\frac{NM}{OM}$(同高三角形的面积比等于底之比).
∴$\frac{PN}{PO}=\frac{NM}{OM}$,
设PN=t,则
$\frac{\sqrt{{t}^{2}+25}}{t}=\frac{2}{3}$,
解得:t=3$\sqrt{5}$.
即点P为(0,-3$\sqrt{5}$).
点评 本题考查了全等三角形的判定与性质,以及勾股定理,正确作出辅助线构造全等的三角形是解决本题的关键.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
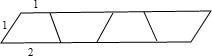
| 梯形个数 | 1 | 2 | 3 | 4 | 5 | 6 | … |
| 周长 | 5 | 8 | 11 | 14 | 17 | 20 | … |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
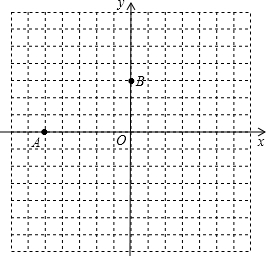 如图,在平面直角坐标系中,已知点A(-5,0),B(0,3)
如图,在平面直角坐标系中,已知点A(-5,0),B(0,3)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在Rt△ABC中,∠C=90°,BC=6cm,AC=8cm,按图中所示方法将△BCD沿BD折叠,使点C落在AB边的C′点.
如图,在Rt△ABC中,∠C=90°,BC=6cm,AC=8cm,按图中所示方法将△BCD沿BD折叠,使点C落在AB边的C′点.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com