
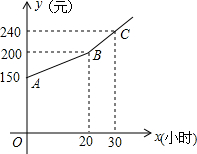
 为了鼓励小强做家务,小强每月的生活总费用都是由基本生活费和上月根据他的家务劳动时间所获得的奖励两部分组成.若设小强每月的家务劳动时间为x小时.下月他可获得的生活总费用为y元,則y(元)和x(小时)之间的函数图象如图所示.
为了鼓励小强做家务,小强每月的生活总费用都是由基本生活费和上月根据他的家务劳动时间所获得的奖励两部分组成.若设小强每月的家务劳动时间为x小时.下月他可获得的生活总费用为y元,則y(元)和x(小时)之间的函数图象如图所示.分析 (1)观察图象可以得出结论;
(2)设出一次函数一般式,代入A、B两点坐标,求解析式即可;
(3)求出BC的解析式,把y=250代入解析式即可.
解答 解:(1)观察图象可得:小强每月的基本生活费是150元,若小强4月份做家务10小时,則他5月份能获得175元生活总费用;
故答案为:150元、175.
(2)设AB段的函数表达式:y=kx+b,将A(0,150)、B(20,200)代入,得:
$\left\{\begin{array}{l}{b=150}\\{20k+b=200}\end{array}\right.$,
解得:
$\left\{\begin{array}{l}{k=2.5}\\{b=150}\end{array}\right.$
所以,AB段的函数关系式是:y=2.5x+150;
(3)设BC段的函数关系式:y=kx+b,则
$\left\{\begin{array}{l}{20k+b=200}\\{30k+b=240}\end{array}\right.$
解得:
$\left\{\begin{array}{l}{k=4}\\{b=120}\end{array}\right.$
所以,BC段的函数关系式:y=4x+120,
把y=250代入,得:x=32.5
所以小强4月份需做家务32.5小时.
点评 本题主要考查了一次函数的图象、待定系数法求函数关系式以及函数的实际应用问题,求出AB段和BC段的函数关系式是解决问题的关键.


科目:初中数学 来源: 题型:选择题
| A. | m>-$\frac{1}{2}$ | B. | m<3 | C. | -$\frac{1}{2}$<m<3 | D. | -$\frac{1}{2}$<m≤3 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,已知三角形ABC,AB=8,BC=10,AC=6,问:
如图,已知三角形ABC,AB=8,BC=10,AC=6,问:查看答案和解析>>
科目:初中数学 来源: 题型:填空题
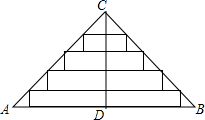 如图,△ABC是一张等腰直角三角形彩色纸,AC=BC=40厘米,若将斜边上的高CD进行五等分,然后裁出4张宽度相等的长方形纸条,则这4张纸条的长度之和是80$\sqrt{2}$厘米.
如图,△ABC是一张等腰直角三角形彩色纸,AC=BC=40厘米,若将斜边上的高CD进行五等分,然后裁出4张宽度相等的长方形纸条,则这4张纸条的长度之和是80$\sqrt{2}$厘米.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
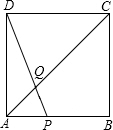 边长为4的正方形ABCD中,点P在边AB上,DP与AC相交于点Q,且△ADQ的面积是正方形ABCD面积的$\frac{1}{6}$,则AP的长为( )
边长为4的正方形ABCD中,点P在边AB上,DP与AC相交于点Q,且△ADQ的面积是正方形ABCD面积的$\frac{1}{6}$,则AP的长为( )| A. | 1.5 | B. | 2 | C. | 3 | D. | 1.25 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 在平面直角坐标系xOy中,将直线y=2x向下平移2个单位后,与一次函数y=-$\frac{1}{2}$x+3的图象相交于点A.
在平面直角坐标系xOy中,将直线y=2x向下平移2个单位后,与一次函数y=-$\frac{1}{2}$x+3的图象相交于点A.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com