
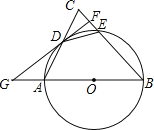
【题目】如图,以AB为直径的⊙O交△ABC的边AC于D、BC于E,过D作⊙O的切线交BC于F,交BA延长线于G,且DF⊥BC.
(1)求证:BA=BC;
(2)若AG=2,cosB=![]() ,求DE的长.
,求DE的长.
【答案】(1)详见解析;(2)![]() .
.
【解析】
(1)连结OD,如图,根据切线的性质得OD⊥DF,而DF⊥BC,根据平行线的判定得到OD∥BC,然后利用平行线的性质和等量代换可得∠OAD=∠C,则根据等腰三角形的判定定理即可得到结论;
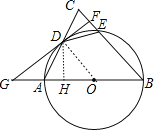
(2)作DH⊥AB于H,如图,设⊙O的半径为r,由平行线的性质得cos∠DOG=cosB=![]() ,则在Rt△ODG中利用余弦可计算出r=3,再在Rt△ODH中利用余弦可求出OH=
,则在Rt△ODG中利用余弦可计算出r=3,再在Rt△ODH中利用余弦可求出OH=![]() ,则AH=
,则AH=![]() ,利用勾股定理可计算出AD,然后证明DE=AD即可.
,利用勾股定理可计算出AD,然后证明DE=AD即可.
(1)证明:连结OD,如图,
∵DF为切线,
∴OD⊥DF,
∵DF⊥BC,
∴OD∥BC,
∴∠ODA=∠C,
而OA=OD,
∴∠ODA=∠OAD,
∴∠OAD=∠C,
∴BA=BC;
(2)作DH⊥AB于H,如图,设⊙O的半径为r,

∵OD∥BC,
∴∠B=∠DOG,
∴cos∠DOG=cosB=![]() ,
,
在Rt△ODG中,∵cos∠DOG=![]() ,即
,即![]() ,
,
∴r=3,
在Rt△ODH中,∵cos∠DOH=![]() ,
,
∴OH=![]() ,
,
∴AH=3﹣![]() =
=![]() ,
,
在Rt△ADH中,AD=![]() ,
,
∵∠DEC=∠C,
∴DE=DC,
而OA=OB,OD∥BC,
∴AD=CD,
∴DE=AD=![]() .
.


 新卷王期末冲刺100分系列答案
新卷王期末冲刺100分系列答案 全能闯关100分系列答案
全能闯关100分系列答案科目:初中数学 来源: 题型:
【题目】如图,某足球运动员站在点O处练习射门,将足球从离地面0.5m的A处正对球门踢出(点A在y轴上),足球的飞行高度y(单位:m)与飞行时间t(单位:s)之间满足函数关系y=at2+5t+c,已知足球飞行0.8s时,离地面的高度为3.5m.
(1)足球飞行的时间是多少时,足球离地面最高?最大高度是多少?
(2)若足球飞行的水平距离x(单位:m)与飞行时间t(单位:s)之间具有函数关系x=10t,已知球门的高度为2.44m,如果该运动员正对球门射门时,离球门的水平距离为28m,他能否将球直接射入球门?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某服装公司试销一种成本为每件50元的![]() 恤衫.试销中发现,当销售单价是60元时,售出400件;销售单价每降低1元,多售出10件.设试销中销售单价
恤衫.试销中发现,当销售单价是60元时,售出400件;销售单价每降低1元,多售出10件.设试销中销售单价![]() (元)时的销售量为
(元)时的销售量为![]() (件).
(件).
(1)求![]() 与
与![]() 之间的函数关系式;
之间的函数关系式;
(2)设该公司获得的总利润为![]() 元,求
元,求![]() 与
与![]() 之间的函数关系式;
之间的函数关系式;
(3)若要销量不低于200件,且获利至少5250元,则售价应在何范围内?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】矩形纸片ABCD,AB=7,BC=4,在矩形边上有一点P,且DP=3.将矩形纸片折叠,使点B与点P重合,折痕所在直线交矩形两边于点E、F,则EF=__________________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点A在线段BD上,在BD的同侧作等腰Rt△ABC和等腰Rt△ADE,其中∠ABC=∠AED=90°,CD与BE、AE分别交于点P、M.对于下列结论:①△CAM∽△DEM;②CD=2BE;③MPMD=MAME;④2CB2=CPCM.其中正确的是( )

A. ①②B. ①②③C. ①②③④D. ①③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,学校的实验楼对面是一幢教学楼,小敏在实验楼的窗口C处测得教学楼顶部D处的仰角为18°,教学楼底部B处的俯角为20°,教学楼的高BD=21m,求实验楼与教学楼之间的距离AB(结果保留整数).(参考数据:tan18°≈0.32,tan20°≈0.36)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,等腰△ABC如图放置,顶角的顶点C在直线m上,分别过点A、B作直线m的垂线,垂足分别为E、D,且AE=CD.
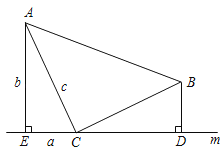
(1)求证:△AEC≌△CDB;
(2)若设△AEC的三边长分別为a、b、c,利用此图证明勾股定理.
查看答案和解析>>
科目:初中数学 来源: 题型:
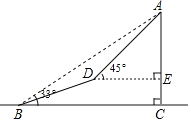
【题目】如图,一座山的一段斜坡BD的长度为600米,且这段斜坡的坡度i=1:3(沿斜坡从B到D时,其升高的高度与水平前进的距离之比).已知在地面B处测得山顶A的仰角为30°,在斜坡D处测得山顶A的仰角为45°.求山顶A到地面BC的高度AC是多少米?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在梯形ABCD中,AD∥BC,EF是梯形ABCD的中位线,若△BEF的面积为4cm2,则梯形ABCD的面积为( )
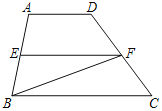
A.8cm2B.12cm2C.16cm2D.20cm2
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com