
【题目】已知,如图:在直角坐标系中,正方形AOBC的边长为4,点D、E分别是线段AO,OC上的动点,D点由A点向O点运动,速度为每秒1个单位,E点由B点向O点运动,速度为每秒2个单位,当一个点停止运动时,另一个点也随之停止.设运动时间为t(秒)
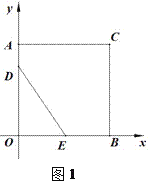
(1)如图1,当t为何值时,△DOE的面积为6;
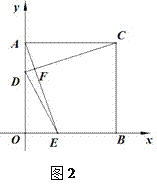
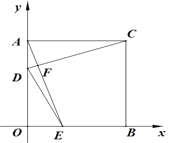
(2)如图2,连结CD,AE交于点F,当t为何值时,CD⊥AE;
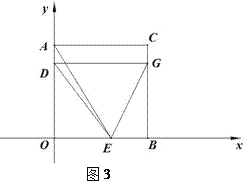
(3)如图3,过点D作DG//OB,交BC于点G,连结EG,当D,E在运动过程中,直角坐标系中是否存在点H,使得点D,E,H,G四点构成的四边形为菱形?若存在,求出t的值,并直接写出点G的坐标,若不存在,请说明理由.
【答案】见解析
【解析】分析:(1)利用三角形的面积公式计算即可;(2)假设CD⊥AE,可得△AOE≌△CAD,由AD=OE,即可求解;(3) 假设存在这样的点H,分两种情况讨论:若DG为菱形的边时;若DG为菱形的对角线时.
详解:(1)如图1,
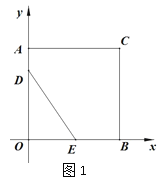
由题意得,AD=t,BE=2t,则OD=4-t,OE=4-2t.
∴S△DOE=![]() =6.
=6.
整理得,![]() .
.
解得,t1=![]() ,t=
,t=![]() (舍去)
(舍去)
∴ 当t为![]() 时,△DOE的面积为6.
时,△DOE的面积为6.
(2)如图2,当CD⊥AE时,此时∠ACD+∠CAF=90°
又∵∠CAF+∠OAE=90°
∴∠ACD=∠OAE
又∵∠AOE=∠CAD=90°,OA=AC
∴△AOE≌△CAD(AAS)
∴AD=OE
即t=4-2t
∴![]()
(3)假设存在这样的点H,使得点D,E,H,G四点构成的四边形为菱形.
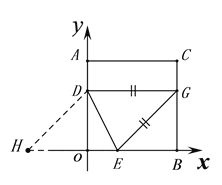
若DG为菱形的边时
①当DE=DG=4时,在Rt△BEG中,![]()
即![]()
∴![]()
∴t1=0,t2=1.6.
当t=0时,此时H刚好与O重合.点G的坐标为(4,4)
当t=1.6时,此时点G的坐标为(4,2.4).
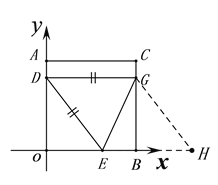
②当DE=DG=4时,在Rt△ODE中,![]()
即![]()
∴![]()
∴ t=0.8或t=4>2(舍去)
当t=0.8时,此时点G的坐标为(4,3.2)
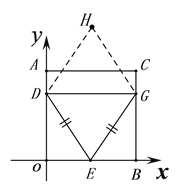
2. 若DG为菱形的对角线时
当DE=DG时,此时OE=BE,即2t=2,∴t=1
此时点G的坐标为(4,3).


 阶梯计算系列答案
阶梯计算系列答案科目:初中数学 来源: 题型:
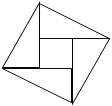
【题目】如图,在北京召开的国际数学家大会会徽取材于我国古代数学家赵爽的《勾股圆方图》
(也称《赵爽弦图》),它是由四个全等的直角三角形与中间的一个小正方形拼成的一个大正方形,如图所示,如果大正方形的面积是13,小正方形式面积是1,直角三角形的短直角边为a,较长直角边为b,那么![]() 的值为________.
的值为________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场欲购进一种商品,当购进这种商品至少为10kg,但不超过30kg时,成本y(元/kg)与进货量x(kg)的函数关系如图所示.
(1)求y关于x的函数解析式,并写出x的取值范围.
(2)若该商场购进这种商品的成本为9.6元/kg,则购进此商品多少千克?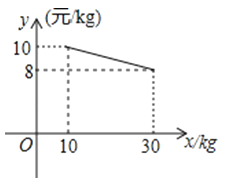
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】端午节期间,某食品店平均每天可卖出300只粽子,卖出1只粽子的利润是1元.经调查发现,零售单价每降0.1元,每天可多卖出100只粽子.为了使每天获取的利润更多,该店决定把零售单价下降m(0<m<1)元.
(1)零售单价下降m元后,该店平均每天可卖出___只粽子,利润为___元;
(2)在不考虑其他因素的条件下,当m定为多少时,才能使该店每天获取的利润是420元,并且卖出的粽子更多?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() 中,
中,![]() ,BD为AC的中线,过点C作
,BD为AC的中线,过点C作![]() 于点E,过点A作BD的平行线,交CE的延长线于点F,在AF的延长线上截取FG=BD,连接 BG,DF.若AF=8,CF=6,则四边形BDFG的周长为_______________.
于点E,过点A作BD的平行线,交CE的延长线于点F,在AF的延长线上截取FG=BD,连接 BG,DF.若AF=8,CF=6,则四边形BDFG的周长为_______________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校组织学生到距离学校6千米的科技馆去参观,小华因事没能乘上学校的包车,于是准备在学校门口改乘出租车去科技馆,出租车收费标准有两种类型,如下表:
里程 | 甲类收费(元) | 乙类收费(元) |
3千米以下(包含3千米) | 7.00 | 6.00 |
3千米以上,每增加1千米 | 1.60 | 1.40 |
(1)设出租车行驶的里程为x千米(![]() 且x取正整数),分别写出两种类型的总收费(用含x的代数式表示);
且x取正整数),分别写出两种类型的总收费(用含x的代数式表示);
(2)小华身上仅有11元,他乘出租车到科技馆车费够不够请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某种型号油电混合动力汽车,从A地到B地燃油行驶纯燃油费用76元,从A地到B地用电行驶纯电费用26元,已知每行驶1千米,纯燃油费用比纯用电费用多0.5元.
(1)求每行驶1千米纯用电的费用;
(2)若要使从A地到B地油电混合行驶所需的油、电费用合计不超过39元,则至少用电行驶多少千米?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com