
【题目】(问题情境)
(1)古希腊著名数学家欧几里得在《几何原本》提出了射影定理,又称“欧几里德定理”:在直角三角形中,斜边上的高是两条直角边在斜边射影的比例中项,每一条直角边又是这条直角边在斜边上的射影和斜边的比例中项.射影定理是数学图形计算的重要定理.
其符号语言是:如图1,在Rt△ABC中,∠ACB=90°,CD⊥AB,垂足为D,则:(1)CD = AD·BD, (2)AC = AB·AD, (3)BC=AB·BD;请你证明定理中的结论(2)BC=AB·BD.
(结论运用)
(2)如图2,正方形ABCD的边长为6,点O是对角线AC、BD的交点,点E在CD上,过点C作CF⊥BE,垂足为F,连接OF,
①求证:△BOF∽△BED;
②若![]() ,求OF的长.
,求OF的长.
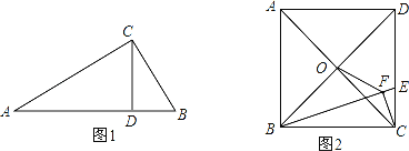
【答案】(1)见解析;(2)①见解析;②![]()
【解析】
(1)通过证明Rt△CBD∽Rt△ABC得到CB:AB=BD:BC,然后利用比例性质即可得到BC=AB·BD;
(2)根据射影定理得BC2=BOBD,BC2=BFBE,则BOBD=BFBE,即![]() ,
,
加上∠OBF=∠EBD,于是可根据相似三角形的判定得到△BOF∽△BED;
(3)先计算出CE 、DE、OB的长,再利用(1)中结论△BOF∽△BED得到
![]() =
=![]() ,即可求得OF的长.
,即可求得OF的长.
(1)证明:如图1,∵CD⊥AB,∠ACB=90°, ∴∠BDC=∠ACB=90°,
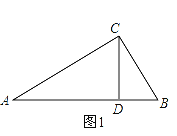
而∠CBD=∠ABC,
∴Rt△CBD ∽Rt△ABC,∴CB:AB=BD:BC,
∴![]() =ABBD;
=ABBD;
(2)①证明:如图2,
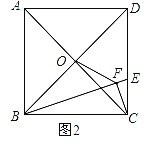
∵四边形ABCD为正方形,
∴OC⊥BO,∠BCD=90°,
∴BC2=BOBD,
∵CF⊥BE,
∴BC2=BFBE,
∴BOBD=BFBE,
即![]() ,
,
而∠OBF=∠EBD,
∴△BOF∽△BED;
②∵在Rt△BCE中,BC=6,![]() ,
,
∴CE=![]() ,∴DE=BC-CE=4,
,∴DE=BC-CE=4,
在Rt△OBC中,OB=![]() ,
,
∵△BOF∽△BED,
∴![]() =
=![]() ,即
,即![]() ,
,
∴OF=![]() .
.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】利客来超市新进一批工艺品,每件的成本是50元,为了合理定价,投放市场进行试销.据市场调查,销售单价是100元时,每天的销售量是50件,而销售单价每降低1元,每天就可多售出5件,但要求销售单价不得低于成本.
(1)求出每天的销售利润w(元)与销售单价x(元)之间的函数关系式;
(2)求出销售单价为多少元时,每天的销售利润为4000元?
(3)如果该企业要使每天的销售利润不低于4000元,且每天的总成本不超过7000元,那么销售单价应控制在什么范围内?(每天的总成本=每件的成本×每天的销售量)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD中,AD∥BC,∠ABC=90°,AB=5,BC=10,连接AC、BD,以BD为直径的圆交AC于点E.若DE=3,则AD的长为________.
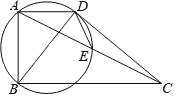
查看答案和解析>>
科目:初中数学 来源: 题型:
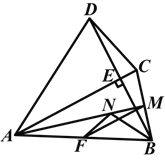
【题目】(2014山东淄博)如图,四边形ABCD中,AC⊥BD交BD于点E,点F,M分别是AB,BC的中点,BN平分∠ABE交AM于点N,AB=AC=BD,连接MF,NF.
(1)判断△BMN的形状,并证明你的结论;
(2)判断△MFN与△BDC之间的关系,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
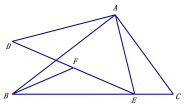
【题目】如图,△ABC∽△ADE,∠BAC =∠ADE =90°,AB=4,AC=3,F是DE的中点,若点E是直线BC上的动点,连接BF,则BF的最小值是_______.
查看答案和解析>>
科目:初中数学 来源: 题型:
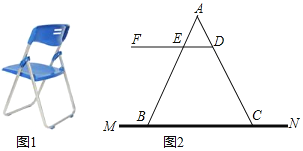
【题目】如图1是一种折叠椅,忽略其支架等的宽度,得到他的侧面简化结构图![]() 图
图![]() ,支架与坐板均用线段表示,若座板DF平行于地面MN,前支撑架AB与后支撑架AC分别与座板DF交于点E、D,现测得
,支架与坐板均用线段表示,若座板DF平行于地面MN,前支撑架AB与后支撑架AC分别与座板DF交于点E、D,现测得![]() 厘米,
厘米, ![]() 厘米,
厘米, ![]() .
.
![]() 求椅子的高度
求椅子的高度![]() 即椅子的座板DF与地面MN之间的距离
即椅子的座板DF与地面MN之间的距离![]() 精确到1厘米
精确到1厘米![]()
![]() 求椅子两脚B、C之间的距离
求椅子两脚B、C之间的距离![]() 精确到1厘米
精确到1厘米![]() 参考数据:
参考数据: ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,等边△ABC内接于⊙O,点P是劣弧![]() 上的一点(端点除外),延长BP至D,使BD=AP,连接CD.
上的一点(端点除外),延长BP至D,使BD=AP,连接CD.

(1)若AP过圆心O,如图①,请你判断△PDC是什么三角形?并说明理由;
(2)若AP不过圆心O,如图②,△PDC又是什么三角形?为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形OABC的顶点O与平面直角坐标系的原点重合,点A,C分别在x轴,y轴上,点B的坐标为(-5,4),点D为边BC上一点,连接OD,若线段OD绕点D顺时针旋转90°后,点O恰好落在AB边上的点E处,则点E的坐标为( )

A. (-5,3) B. (-5,4) C. (-5,![]() ) D. (-5,2)
) D. (-5,2)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=ax2+bx﹣3a经过点A(﹣1,0)、C(0,3),与x轴交于另一点B,抛物线的顶点为D.

(1)求此二次函数解析式;
(2)连接DC、BC、DB,求证:△BCD是直角三角形;
(3)在对称轴右侧的抛物线上是否存在点P,使得△PDC为等腰三角形?若存在,求出符合条件的点P的坐标;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com