
【题目】利客来超市新进一批工艺品,每件的成本是50元,为了合理定价,投放市场进行试销.据市场调查,销售单价是100元时,每天的销售量是50件,而销售单价每降低1元,每天就可多售出5件,但要求销售单价不得低于成本.
(1)求出每天的销售利润w(元)与销售单价x(元)之间的函数关系式;
(2)求出销售单价为多少元时,每天的销售利润为4000元?
(3)如果该企业要使每天的销售利润不低于4000元,且每天的总成本不超过7000元,那么销售单价应控制在什么范围内?(每天的总成本=每件的成本×每天的销售量)
【答案】(1)![]() (2)销售价为70元或90元时,利润4000元;(3)
(2)销售价为70元或90元时,利润4000元;(3)![]() 元
元
【解析】
(1)根据“利润=(售价-成本)×销售量”列出方程;
(2)根据单件利润×销售量=总利润,列方程求解可得;
(3)把y=4000代入函数解析式,求得相应的x值;然后由“每天的总成本不超过7000元”列出关于x的不等式50(-5x+550)≤7000,通过解不等式来求x的取值范围.
解:(1)W=(x-50)[50+5(100-x)]
=(x-50)(-5x+550)
=-5x2+800x-27500
∴W=-5x2+800x-27500(50≤x≤100);
(2):设销售单价为x元,
由题意,得:(x-50)[50+5(100-x)]=4000,
整理,得:x2-160x+6300=0,
解之,得:x=70或x=90,均符合题意,
所以,销售单价为70元或90元时,每天的销售利润可达4000元;
(3)当y=4000时,-5(x-80)2+4500=4000,
解得x1=70,x2=90.
∴当70≤x≤90时,每天的销售利润不低于4000元.
由每天的总成本不超过7000元,得50(-5x+550)≤7000,
解得x≥82.
∴82≤x≤90,
∵50≤x≤100,
∴销售单价应该控制在82元至90元之间.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】已知MN∥EF∥BC,点A、D为直线MN上的两动点,AD=a,BC=b,AE∶ED=m∶n;
(1)当点A、D重合,即a=0时(如图1),试求EF.(用含m,n,b的代数式表示)
(2)请直接应用(1)的结论解决下面问题:当A、D不重合,即a≠0,
①如图2这种情况时,试求EF.(用含a,b,m,n的代数式表示)
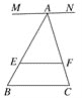
图1
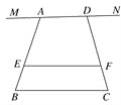
图2
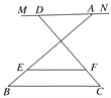
图3
②如图3这种情况时,试猜想EF与a、b之间有何种数量关系?并证明你的猜想.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=ax2+bx+c的图象如图所示,则下列结论:①ac>0;②a﹣b+c<0;③当x<0时,y<0;④方程ax2+bx+c=0(a≠0)有两个大于﹣1的实数根.其中正确的结论有( )
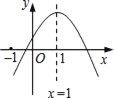
A. ①③ B. ②③ C. ①④ D. ②④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场将每件进价为80元的A商品按每件100元出售,一天可售出128件.经过市场调查,发现这种商品的销售单价每降低1元,其日销量可增加8件.设该商品每件降价x元,商场一天可通过A商品获利润y元.
(1)求y与x之间的函数解析式(不必写出自变量x的取值范围)
(2)A商品销售单价为多少时,该商场每天通过A商品所获的利润最大?
查看答案和解析>>
科目:初中数学 来源: 题型:
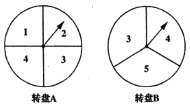
【题目】甲、乙两人在玩转盘游戏时,把两个可以自由传动的转盘A,B分别分成4等份,3等份的扇形区域,并在每一小区域内标上数字(如图所示).游戏规则:同时转动两个转盘,当转盘停止后,若指针所指两个区域的数字之和为奇数,则甲胜;若指针所指两个区域的数字之和为偶数,则乙胜.如果指针落在分割线上,则需要重新转动转盘.请问这个游戏规则对甲、乙双方公平吗?试说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
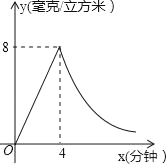
【题目】为了预防“流感”,某学校对教室采用药熏法进行消毒,已知药物燃烧时,室内每立方米空气中的含药量y(毫克/立方米)与药物点燃后的时间x(分钟)成正比例,药物燃尽后,y与x成反比例(如图所示).已知药物点燃后4分钟燃尽,此时室内每立方米空气中含药量为8毫克.
(1)求药物燃烧时,y与x之间函数的表达式;
(2)求药物燃尽后,y与x之间函数的表达式;
(3)研究表明,当空气中每立方米的含药量不低于2毫克时,才能有效杀灭空气中的病菌,那么此次消毒有效时间有多长?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图工程上常用钢珠来测量零件上小圆孔的宽口,假设钢珠的直径是10mm,测得钢珠顶端离零件表面的距离为8mm,如图所示.则这个小圆孔的宽口AB的长度是( )
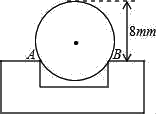
A. 5mm B. 6mm C. 8mm D. 10mm
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,下面是二次函数![]() 图象的一部分,则下列结论中:①
图象的一部分,则下列结论中:①![]() ;②
;②![]() ③方程
③方程![]() 有两个不等的实数根;④
有两个不等的实数根;④![]() .正确的个数是( )
.正确的个数是( )
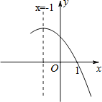
A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(问题情境)
(1)古希腊著名数学家欧几里得在《几何原本》提出了射影定理,又称“欧几里德定理”:在直角三角形中,斜边上的高是两条直角边在斜边射影的比例中项,每一条直角边又是这条直角边在斜边上的射影和斜边的比例中项.射影定理是数学图形计算的重要定理.
其符号语言是:如图1,在Rt△ABC中,∠ACB=90°,CD⊥AB,垂足为D,则:(1)CD = AD·BD, (2)AC = AB·AD, (3)BC=AB·BD;请你证明定理中的结论(2)BC=AB·BD.
(结论运用)
(2)如图2,正方形ABCD的边长为6,点O是对角线AC、BD的交点,点E在CD上,过点C作CF⊥BE,垂足为F,连接OF,
①求证:△BOF∽△BED;
②若![]() ,求OF的长.
,求OF的长.
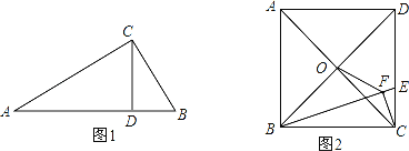
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com