
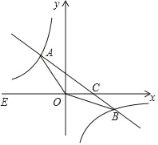
【题目】如图,在平面直角坐标系xOy中,双曲线y=![]() (k≠0)与直线y=
(k≠0)与直线y=![]() 的交点为A(a,﹣1),B(2,b)两点,双曲线上一点P的横坐标为1,直线PA,PB与x轴的交点分别为点M,N,连接AN.
的交点为A(a,﹣1),B(2,b)两点,双曲线上一点P的横坐标为1,直线PA,PB与x轴的交点分别为点M,N,连接AN.
(1)直接写出a,k的值;
(2)求证:PM=PN,PM⊥PN.
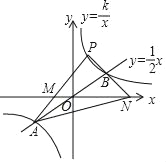
【答案】(1)k=2;(2)详见解析;
【解析】
(1)依据双曲线y=![]() (k≠0)与直线y=
(k≠0)与直线y=![]() 的交点为A(a,﹣1),B(2,b)两点,可得点A与点B关于原点对称,进而得到a,k的值;
的交点为A(a,﹣1),B(2,b)两点,可得点A与点B关于原点对称,进而得到a,k的值;
(2)根据双曲线y=![]() 上一点P的横坐标为1,可得点P的坐标为(1,2),进而得到直线PA,PB的函数表达式分别为y=x+1,y=﹣x+3,求得直线PA,PB与x轴的交点坐标分别为M(﹣1,0),N(3,0),即可得到PM=PN,PM⊥PN.
上一点P的横坐标为1,可得点P的坐标为(1,2),进而得到直线PA,PB的函数表达式分别为y=x+1,y=﹣x+3,求得直线PA,PB与x轴的交点坐标分别为M(﹣1,0),N(3,0),即可得到PM=PN,PM⊥PN.
解:(1)∵双曲线y=![]() (k≠0)与直线y=
(k≠0)与直线y=![]() 的交点为A(a,﹣1),B(2,b)两点,
的交点为A(a,﹣1),B(2,b)两点,
∴点A与点B关于原点对称,
∴a=﹣2,b=1,
∴把A(﹣2,﹣1)代入双曲线y=![]() ,可得k=2;
,可得k=2;
(2)证明:∵双曲线y=![]() 上一点P的横坐标为1,
上一点P的横坐标为1,
∴点P的坐标为(1,2),
∴直线PA,PB的函数表达式分别为y=x+1,y=﹣x+3,
∴直线PA,PB与x轴的交点坐标分别为M(﹣1,0),N(3,0),
∴PM=2![]() ,PN=2
,PN=2![]() ,MN=4,
,MN=4,
∴PM=PN,PM2+PN2=MN2,
∴∠MPN=90°,
∴PM⊥PN.


科目:初中数学 来源: 题型:
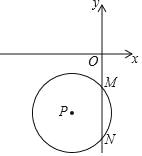
【题目】如图,半径为5的⊙P与y轴交于点M(0,﹣4),N(0,﹣10)
(1)求点P的坐标;
(2)将⊙P绕点O顺时针方向旋转90°后得⊙A,交x轴于B、C,求过A、B、C三个点的抛物线的解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知∠MON=30°,B为OM上一点,BA⊥ON于A,四边形ABCD为正方形,P为射线BM上一动点,连结CP,将CP绕点C顺时针方向旋转90°得CE,连结BE,若AB=4,则BE的最小值为_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
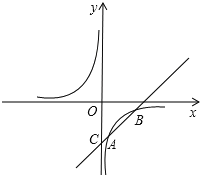
【题目】如图,已知反比例函数y =![]() 的图象经过点A(1,-3),一次函数y =kx +b的图象经过点A与点C(0,-4),且与反比例函数的图象相交于另一点B.试确定点B的坐标.
的图象经过点A(1,-3),一次函数y =kx +b的图象经过点A与点C(0,-4),且与反比例函数的图象相交于另一点B.试确定点B的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,A,B两点的坐标分别为A(2,2),B(2,﹣2).对于给定的线段AB及点P,Q,给出如下定义:若点Q关于AB所在直线的对称点Q′落在△ABP的内部(不含边界),则称点Q是点P关于线段AB的内称点.
(1)已知点P(4,﹣1).
①在Q1(1,﹣1),Q2(1,1)两点中,是点P关于线段AB的内称点的是 ;
②若点M在直线y=x﹣1上,且点M是点P关于线段AB的内称点,求点M的横坐标xM的取值范围;
(2)已知点C(3,3),⊙C的半径为r,点D(4,0),若点E是点D关于线段AB的内称点,且满足直线DE与⊙C相切,求半径r的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,抛物线C1:y=mx2﹣2mx+m+4与y轴交于点A(0,3),与x轴交于点B、C(点B在点C左侧).
(1)求该抛物线的解析式;
(2)求点B的坐标;
(3)若抛物线C2:y=a(x﹣1)2﹣1(a≠0)与线段AB恰有一个公共点,结合函数的图象,求a的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy的中,一次函数y=kx+b(k≠0)的图象与反比例函数y=![]() (m≠0)的图象交于二、四象限内的A、B两点,与x轴交于C点,点B的坐标为(6,n),线段OA=
(m≠0)的图象交于二、四象限内的A、B两点,与x轴交于C点,点B的坐标为(6,n),线段OA=![]() ,E为x轴上一点,且tan∠AOE=
,E为x轴上一点,且tan∠AOE=![]()
(1)求该反比例函数和一次函数的解析式;
(2)求△A0B的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的方程x2+mx+m﹣3=0.
(1)若该方程的一个根为2,求m的值及方程的另一个根;
(2)求证:不论m取何实数,该方程都有两个不相等的实数根.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com