
����Ŀ����ƽ��ֱ������ϵxOy�У�A��B���������ֱ�ΪA��2��2����B��2����2�������ڸ������߶�AB����P��Q���������¶��壺����Q����AB����ֱ�ߵĶԳƵ�Q�����ڡ�ABP���ڲ��������߽磩����Ƶ�Q�ǵ�P�����߶�AB���ڳƵ㣮
��1����֪��P��4����1����
����Q1��1����1����Q2��1��1�������У��ǵ�P�����߶�AB���ڳƵ������ ����
������M��ֱ��y��x��1�ϣ��ҵ�M�ǵ�P�����߶�AB���ڳƵ㣬���M�ĺ�����xM��ȡֵ��Χ��
��2����֪��C��3��3������C�İ뾶Ϊr����D��4��0��������E�ǵ�D�����߶�AB���ڳƵ㣬������ֱ��DE����C���У���뾶r��ȡֵ��Χ��
���𰸡���1����Q1����0��xM��2����2��![]() ��r��
��r��![]() ��
��
��������
��1���������ڶԳƵ�����弴�ɵó����ۣ�
�����жϳ���O����ֱ��AB�ĶԳƵ�P'��ֱ��y��x��1�ϣ������жϳ����ۣ�
��2���жϳ�DE��ԲC����ʱ��ԲC���İ뾶����С��λ�ã����㼴�ɵó����ۣ�
�⣺��1����
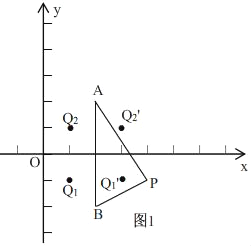
����ͼ�Σ����ڶԳƵ������ã���P�����߶�AB���ڳƵ����Q1��
�ʴ�ΪQ1��
����ͼ2��
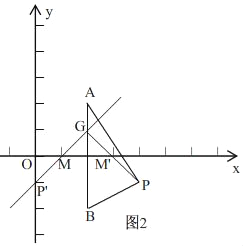
��P��4����1������AB����ֱ�ߵĶԳƵ�P'��0����1������ʱ����P'ǡ����ֱ��y��x��1�ϣ�
�ߵ�M�ǵ�P�����߶�AB���ڶԳƵ㣬
���M����AB����ֱ�ߵĶԳƵ�M'������ABP�ڲ��������߽磩��
�ߵ�M��ֱ��y��x��1�ϣ�
���MӦ���߶�P'G�ϣ���GΪ�߶�AB��ֱ��y��x��1�Ľ��㣩���Ҳ��������˵�P'��G�غϣ�
��0��xM��2��
��2����ͼ3��
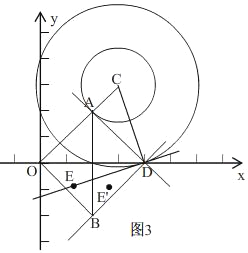
�ߵ�E�ǵ�D�����߶�AB���ڳƵ㣬
���E����AB����ֱ�ߵĶԳƵ�E'Ӧ����ABD�ڲ��������߽磩��
�ߵ�D����AB����ֱ�ߵĶԳƵ�Ϊԭ��O��
���EӦ����ABO���ڲ��������߽磩��
��A��2��2����C��3��3����D��4��0����
��AC��![]() ��AD��2
��AD��2![]() ��CD��
��CD��![]() ��
��
��AC2+AD2��CD2��
���CAD��90�㣬
��AC��AD��
��ʱ��ֱ��DA����ACΪ�뾶�ġ�C���У��뾶AC��![]() ��
��
��ֱ��DE����CDΪ�뾶�ġ�C���У���DΪ�е㣬��C�İ뾶������ֵΪ![]() ��
��
���������ġ�C�İ뾶r��ȡֵ��Χ��![]() ��r��
��r��![]() ��
��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������˵����ȷ���ǣ� ��
A. Ϊ�˽���������ѧ����˯�������Ӧ�ò����ղ�ķ�ʽ
B. ij�ֲ�Ʊ���н�������![]() ������
������![]() �����ֲ�Ʊһ�����н�
�����ֲ�Ʊһ�����н�
C. һ������![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ���������������
���������������![]()
D. ���������ݵķ���![]() ���������ݵķ���
���������ݵķ���![]() �����������ݱȼ��������ȶ�
�����������ݱȼ��������ȶ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ijũ����������һ��ũ����Ʒ����֪���ֲ�Ʒ�ijɱ���Ϊ20Ԫ/ǧ�ˣ��г����鷢�֣��ò�Ʒÿ���������w ��ǧ�ˣ������ۼ�x ��Ԫ/ǧ�ˣ������¹�ϵ��w=��2x+80�������ֲ�Ʒÿ�����������Ϊy ��Ԫ����
��1����y��x֮��ĺ�����ϵʽ���Ա���x��ȡֵ��Χ��
��2�������ۼ۶�Ϊ����Ԫʱ��ÿ����������������������Ƕ��٣�
��3�������۲��Ź涨���ֲ�Ʒ�����ۼ۲��ø���28Ԫ/ǧ�ˣ���ũ����Ҫÿ����150Ԫ�������������ۼ�Ӧ��Ϊ����Ԫ�����ο���ϵ�����۶�=�ۼۡ�����������=���۶�ɱ���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��Rt��ABO�Ķ���A��˫����y��![]() ��ֱ��y����x��(k��1)�ڵڶ����Ľ��㣮AB��x����B����S��ABO��
��ֱ��y����x��(k��1)�ڵڶ����Ľ��㣮AB��x����B����S��ABO��![]() ��
��
(1)�������������Ľ���ʽ��
(2)��ֱ����˫���ߵ���������A��C���������AOC�������

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
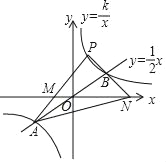
����Ŀ����ͼ����ƽ��ֱ������ϵxOy�У�˫����y��![]() ��k��0����ֱ��y��
��k��0����ֱ��y��![]() �Ľ���ΪA��a����1����B��2��b�����㣬˫������һ��P�ĺ�����Ϊ1��ֱ��PA��PB��x��Ľ���ֱ�Ϊ��M��N������AN��
�Ľ���ΪA��a����1����B��2��b�����㣬˫������һ��P�ĺ�����Ϊ1��ֱ��PA��PB��x��Ľ���ֱ�Ϊ��M��N������AN��
��1��ֱ��д��a��k��ֵ��
��2����֤��PM��PN��PM��PN��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
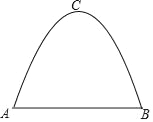
����Ŀ��һ������������������������ͼ��ʾ�������й�·�Ŀ���AB��8m����������ߵ�C����·�ľ���Ϊ6m��
��1�������ʵ���ƽ��ֱ������ϵ���������ߵı���ʽ��
��2������һ�������ĸ߶���4.4m�������Ŀ�����2m��Ϊ�˱�֤��ȫ����������������������0.5m��ͨ������˵�����������ܷ�ȫͨ������������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
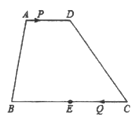
����Ŀ����ͼ�����ı���![]() �У�
�У�![]() ,
, ![]() ��
��![]() ���е�.��
���е�.��![]() ��ÿ��1����λ���ȵ��ٶȴӵ�
��ÿ��1����λ���ȵ��ٶȴӵ�![]() ��������
��������![]() ���
���![]() �˶�;��
�˶�;��![]() ͬʱ��ÿ��3����λ���ȵ��ٶȴ� ��
ͬʱ��ÿ��3����λ���ȵ��ٶȴ� ��![]() ��������
��������![]() ���
���![]() �˶�.��
�˶�.��![]() ֹͣ�˶�ʱ����
ֹͣ�˶�ʱ����![]() Ҳ��ֹ֮ͣ�˶�.���˶�ʱ��
Ҳ��ֹ֮ͣ�˶�.���˶�ʱ��![]() ��ʱ���Ե�
��ʱ���Ե�![]() Ϊ������ı�����ƽ���ı���.��
Ϊ������ı�����ƽ���ı���.��![]() ��ֵΪ_________.
��ֵΪ_________.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����![]() ��
��![]() �ֱ������
�ֱ������![]() �����ϵĵ㣬�ֱ��Ե�
�����ϵĵ㣬�ֱ��Ե�![]() ��
��![]() ΪԲ�ģ���
ΪԲ�ģ���![]() ��
��![]() �ij�Ϊ�뾶�����������ཻ�ڵ�
�ij�Ϊ�뾶�����������ཻ�ڵ�![]() ������
������![]() ��
��![]() ��
��

��1�������ж������ı��ε���״����˵�����ɣ�
��2����![]() �����жϴ��ı��ε���״����˵�����ɣ�
�����жϴ��ı��ε���״����˵�����ɣ�
��3���ڣ�2���������£�����![]() ����
����![]() ���ף�
���ף�![]() �����߶�
�����߶�![]() �ij���
�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪ABCD���ĸ��ڽǵ�ƽ���߷ֱ��ཻ�ڵ�E��F��G��H������AC����EF=2��FG=GC=5����AC�ij��ǣ�������

A. 12 B. 13 C. ![]() D.
D. ![]()
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com