
����Ŀ����֪��ԭ��O����ֱ����Բ��ΪM��0��4�����뾶Ϊ2��Բ���У��е�ֱ�ΪP��Q��PQ��y���ڵ�K�������߾���P��Q���㣬����ΪN��0��6��������x�ύ��A��B���㣮 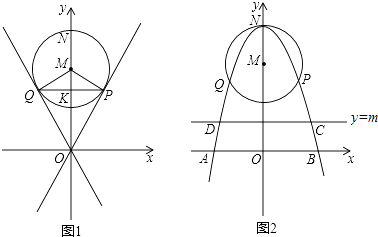
��1�����P�����ꣻ
��2���������߽���ʽ��
��3����ֱ��y=nx+m�У���n=0��m��0ʱ��y=m��ƽ����x���ֱ�ߣ���ֱ��y=m���������ཻ�ڵ�C��D������ֱ�����M����ʱ�����A��B��C��DΧ�ɵĶ���ε����������������ţ���
���𰸡�
��1���⣺��ͼ1��
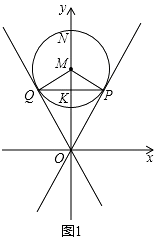
�ߡ�M��OP�����ڵ�P��
��MP��OP������MPO=90�㣮
�ߵ�M��0��4����OM=4��MP=2��
��OP=2 ![]() ��
��
�ߡ�M��OP�����ڵ�P����M��OQ�����ڵ�Q��
��OQ=OP����POK=��QOK��
��OK��PQ��QK=PK��
��PK= ![]() =
= ![]() =
= ![]() ��
��
��OK= ![]() =3��
=3��
���P�������� ![]() ��3��
��3��
��2���⣺��ͼ2��
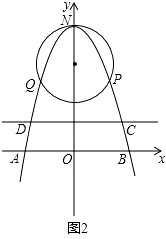
�趥��Ϊ��0��6���������ߵĽ���ʽΪy=ax2+6��
�ߵ�P�� ![]() ��3����������y=ax2+6�ϣ�
��3����������y=ax2+6�ϣ�
��3a+6=3��
��ã�a=��1��
��������ߵĽ���ʽΪy=��x2+6
��3���⣺��ֱ��y=m���M����ʱ��
���� ![]() =2��
=2��
��ã�m1=2��m2=6��
��m=2ʱ����ͼ3��
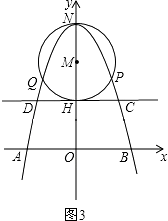
����OH=2��
��y=2ʱ���ⷽ�̩�x2+6=2�ã�x=��2��
���C��2��2����D����2��2����CD=4��
ͬ���ɵã�AB=2 ![]() ��
��
��S����ABCD= ![]() ��DC+AB��OH=
��DC+AB��OH= ![]() ��4+2
��4+2 ![]() ����2=4+2
����2=4+2 ![]() ��
��
��m=6ʱ����ͼ4��
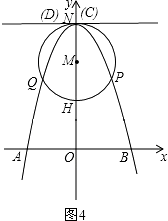
��ʱ��C����D���N�غϣ�
S��ABC= ![]() ABOC=
ABOC= ![]() ��2
��2 ![]() ��6=6
��6=6 ![]() ��
��
������������A��B��C��DΧ�ɵĶ���ε����Ϊ4+2 ![]() ��6
��6 ![]()
����������1�������ߵ����ʿɡ�MPO=90�㣬���ݹ��ɶ��������PO��Ȼ��������������PK��Ȼ�����ù��ɶ��������OK���Ϳɵõ���P�����꣮��2�����趥��Ϊ��0��6���������ߵĽ���ʽΪy=ax2+6��Ȼ��P���������Ϳ���������ߵĽ���ʽ����3��ֱ��y=m���M���������ֿ��ܣ�ֻ�������������ֱ����۾Ϳ������Ӧ����ε������
�����㾫����ͨ������������߳������͵��������ε����ʣ����մ�Բ��һ����Բ���������ߣ����ǵ����߳����Բ�ĺ���һ�������ƽ���������ߵļнǣ����������ε���������ȣ���ƣ��ȱ߶ԵȽǣ������Խ����⣮


 ��ʱѵ���������������ϵ�д�
��ʱѵ���������������ϵ�д� �ƸԾ���Ȥζ����ϵ�д�
�ƸԾ���Ȥζ����ϵ�д� ����С����ҵ��ϵ�д�
����С����ҵ��ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������{a��b��c}Ϊ����y=ax2+bx+c�ġ�����������
��1������������Ϊ{��1��2��3}�ĺ�������ʽΪ �� ������������Ϊ{0��1��1}�ĺ�������ƽ��������λ�Ժ�õ��ĺ�������ʽΪ��
��2�����ǰѺᡢ�������Ϊ�����ĵ��Ϊ�����㡱�����ʣ�������������д�ĺ���ͼ��Χ�ɵķ��ͼ�Σ������߽磩�ڹ��ж��ٸ����㣿�������ϸ��������̣�
��3�����塰�������������㣺��{a1 �� b1 �� c1}+{a2 �� b2 �� c2}={a1+a2 �� b1+b2 �� c1+c2}���ڦ�{a1 �� b1 �� c1}={��a1 �� ��b1 �� ��c1}�����Ц�Ϊ���ⳣ���������ʣ�����������Ϊ{��1��2��3}+��{0��1����1}�ĺ����Ƿ�����㣿��������㣬�������ö������ꣻ��������ڣ���˵��������ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ֱ֪��l��y=kx+b��k��0����ͼ����x�ᡢy�ύ��A��B���㣬A����2��0����B��0��1����
��1����ֱ��l�ĺ�������ʽ��
��2����P��x���ϵ�һ�����㣬��ֱ��д������PAB�ǵ���������ʱP�����ꣻ
��3����y�����е�C��0��3������D��ֱ��l�ϣ�����ACD�������4�����D�����꣮

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����м������У�ͬһ�������������ͼ�븩��ͼ��ͬ���ǣ� ��
A.![]() Բ��
Բ��
B. ������
������
C. Բ
Բ
D. ��
��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ڱ�Ϊ��1��������ɵ������У�����ƽ��ֱ������ϵ����A����4��2����B����2��3����C����1��1��������ABC����x�ᷭ�ۺõ���DEF����B�ĶԳƵ��ǵ�E�������E�ķ�������������ʽ����д�����������ڸ÷���������ͼ�������������и������꣮ 
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����2�������ƻ���һ���£�30�죩����װ520̨��Ʒ��ÿ���Ʒ�IJ�����ͬ������ԭ�ȵ���װ�ٶȣ���������������Ӱ�������ÿ��������ÿ�����װ2̨��Ʒ������ǰ�������
��1��ÿ��������ԭ��ÿ���������װ����̨��Ʒ��
��2��Ҫ���ƻ����������һ������1�������ߣ���Ҫ��Ͷ��19000Ԫ�����Զ�����ÿ������װ���̨���Ӱ�������ÿ��������ÿ�칲Ҫ���350Ԫ��ѡ��һ�����Խ�ʡ���ã�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪�ı���ABCDΪ�������Σ�AD��BC��AB=CD��AD= ![]() ��EΪCD�е㣬����AE����AE=2
��EΪCD�е㣬����AE����AE=2 ![]() ����DAE=30�㣬��AE��AF��BC��F����BF=�� ��
����DAE=30�㣬��AE��AF��BC��F����BF=�� �� 
A.1
B.3�� ![]()
C.![]() ��1
��1
D.4��2 ![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵ�У���M��ԭ��O����x�ύ��A��4��0������y�ύ��B��0��3������CΪ�ӻ�AO���е㣬����AC���ӳ���D��ʹDC=4CA������BD�� 
��1�����M�İ뾶��
��2��֤����BDΪ��M�����ߣ�
��3����ֱ��MC����һ��P��ʹ|DP��AP|���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����һ�а�һ��˳��������е�����
��һ������ ![]() ��
��
�ڶ������� ![]() ��
��
���������� ![]() ��
��
��
���κ�������n����n������ڣ�n+1�������ĺ͵��� ![]() ��
��
��1������̽�������Ƿ��֣� ![]()
���������ĵ�5����Ϊa����ô ![]() ��
�� ![]() ��
�� ![]() ���ĸ���ȷ��
���ĸ���ȷ��
����ֱ��д����ȷ�Ľ��ۣ�
��2������۲��1��������2��������3�����������������ĵ�n����������������n��ʾ��n����������֤����IJ������㡰��n������ڣ�n+1�������ĺ͵��� ![]() ����
����
��3����M��ʾ ![]() ��
�� ![]() ��
�� ![]() ������
������ ![]() ����2016�����ĺͣ���
����2016�����ĺͣ��� ![]() ��
��
��֤�� ![]() ��
��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com