
【题目】如图,PA、PB、AB都与⊙O相切,∠P=60°,则∠AOB等于( ) 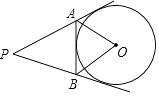
A.50°
B.60°
C.70°
D.70°
【答案】B
【解析】解:设PA、PB、AB与⊙O相切于E、D、C,连接OE、OD、OC,如图, ∴PA、PB、AB都与⊙O相切,
∴OE⊥AB,OD⊥PB,OC⊥PA,
∴∠COD=180°﹣∠P=120°,
在Rt△AOC和Rt△AOE中![]() ,
,
∴Rt△AOC≌Rt△AOE,
同理可得△OBD≌△OBE,
∴∠AOC=∠AOE,∠BOD=∠BOE,
∴∠AOB= ![]() COD=60°.
COD=60°.
故选B.
设PA、PB、AB与⊙O相切于E、D、C,连接OE、OD、OC,如图,根据切线的性质得OE⊥AB,OD⊥PB,OC⊥PA,利用四边形的内角和可计算出∠COD=120°,再证△OAC≌△OAE,△OBD≌△OBE得到∠AOC=∠AOE,∠BOD=∠BOE,所以∠AOB= ![]() COD=60°.
COD=60°.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】(阅读)数轴上点A、B表示的数分别是a、b,若a>b,则AB=a﹣b.

例如,若数轴上点A、B表示的两个数分别为﹣2000和+18,
则AB=18﹣(﹣2000)=18+2000=2018
(应用)若数轴上点A、B表示的两个数分别为x和﹣1,且x>﹣1,则AB= (用含x的代数式表示);
(拓展)如图,数轴上点A表示的数为﹣2a,点B表示的数为﹣![]() a,点C表示的数为﹣2,且AB=BC.
a,点C表示的数为﹣2,且AB=BC.
(1)求a的值;
(2)以BC为边作等边三角形BCD,并将共向右滚动1周得到新的等边三角形BCD,依次继续滚动…….若滚动第n周后,等边三角形BCD的顶点C表示的数是2014,求n的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知直线y= ![]() x与双曲线y=
x与双曲线y= ![]() (k>0)交于A、B两点,点B的坐标为(﹣4,﹣2),C为双曲线y=
(k>0)交于A、B两点,点B的坐标为(﹣4,﹣2),C为双曲线y= ![]() (k>0)上一点,且在第一象限内,若△AOC的面积为6,则点C的坐标为( )
(k>0)上一点,且在第一象限内,若△AOC的面积为6,则点C的坐标为( ) 
A.(2,4)
B.(1,8)
C.(2,4)或(1,8)
D.(2,4)或(8,1)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读材料,在平面直角坐标系中,已知x轴上两点A(x1,0),B(x2,0)的距离记作AB=|x1﹣x2|;若A,B是平面上任意两点,我们可以通过构造直角三角形来求AB间的距离,如图,过A,B分别向x轴、y轴作垂线AM1、AN1和BM2、BN2,垂足分别是M1、N1、M2、N2,直线AN1交BM2于点Q,在Rt△ABQ中,AQ=|x1﹣x2|,BQ=|y1﹣y2|,∴AB2=AQ2+BQ2=|x1﹣x2|+|y1﹣y2|2=(x1﹣x2)2+(y1﹣y2)2,由此得到平面直角坐标系内任意两点A(x1,y1),B(x2,y2)间的距离公式为:
(1)AB= .
(2)直接应用平面内两点间距离公式计算点A(1,﹣3),B(﹣2,1)之间的距离为 ;
(3)根据阅读材料并利用平面内两点间的距离公式,求代数式![]() 的最小值.
的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图(1),已知正方形ABCD在直线MN的上方,BC在直线MN上,E是BC上一点,以AE为边在直线MN的上方作正方形AEFG. 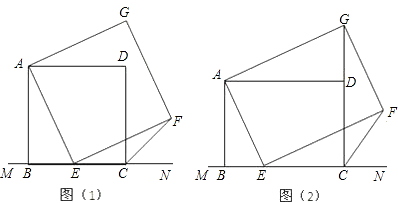
(1)连接GD,求证:△ADG≌△ABE;
(2)连接FC,观察并猜测∠FCN的度数,并说明理由;
(3)如图(2),将图(1)中正方形ABCD改为矩形ABCD,AB=a,BC=b(a、b为常数),E是线段BC上一动点(不含端点B、C),以AE为边在直线MN的上方作矩形AEFG,使顶点G恰好落在射线CD上.判断当点E由B向C运动时,∠FCN的大小是否总保持不变?若∠FCN的大小不变,请用含a、b的代数式表示tan∠FCN的值;若∠FCN的大小发生改变,请举例说明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,放在直角坐标系中的正方形ABCD边长为4,现做如下实验:抛掷一枚均匀的正四面体骰子(它有四个顶点,各顶点的点数分别是1至4这四个数字中一个),每个顶点朝上的机会是相同的,连续抛掷两次,将骰子朝上的顶点数作为直角坐标中P点的坐标)第一次的点数作横坐标,第二次的点数作纵坐标). 
(1)求P点落在正方形ABCD面上(含正方形内部和边界)的概率.
(2)将正方形ABCD平移整数个单位,则是否存在一种平移,使点P落在正方形ABCD 面上的概率为 ![]() ;若存在,指出其中的一种平移方式;若不存在,请说明理由.
;若存在,指出其中的一种平移方式;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将5个完全相同的小球分装在甲、乙两个不透明的口袋中.甲袋中有3个球,分别标有数字2,3,4;乙袋中有2个球,分别标有数字2,4.从甲、乙两个口袋中各随机摸出一个球.
(1)用列表法或画树状图法,求摸出的两个球上数字之和为5的概率.
(2)摸出的两个球上数字之和为多少时的概率最大?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】煤气公司一工人检修一条长540米的煤气管道,计划用若干小时完成,在实际检修过程中,每小时检修的管道长度是原计划的1.5倍,结果提前3小时完成任务,求该工人原计划每小时检修煤气管道多少米?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com