
【题目】(阅读)数轴上点A、B表示的数分别是a、b,若a>b,则AB=a﹣b.

例如,若数轴上点A、B表示的两个数分别为﹣2000和+18,
则AB=18﹣(﹣2000)=18+2000=2018
(应用)若数轴上点A、B表示的两个数分别为x和﹣1,且x>﹣1,则AB= (用含x的代数式表示);
(拓展)如图,数轴上点A表示的数为﹣2a,点B表示的数为﹣![]() a,点C表示的数为﹣2,且AB=BC.
a,点C表示的数为﹣2,且AB=BC.
(1)求a的值;
(2)以BC为边作等边三角形BCD,并将共向右滚动1周得到新的等边三角形BCD,依次继续滚动…….若滚动第n周后,等边三角形BCD的顶点C表示的数是2014,求n的值.
【答案】【应用】:x+1;【拓展】(1)3;(2)336.
【解析】
(应用)中,根据题意可以用含x的代数式表示出AB;
(拓展)(1)根据题意可以得到关于a的方程,从而可以求得a的值;
(2)根据题意和数轴可以得到三角形滚动一周点C的变化,从而可以求得滚动n周的变化情况,从而可以求得n的值.
解:(应用)若数轴上点A、B表示的两个数分别为x和﹣1,且x>﹣1,
则AB=x-(-1)=x+1,
(拓展)(1)∵数轴上点A表示的数为-2a,点B表示的数为数轴上点A表示的数为-2a,点B表示的数为![]() a,点C表示的数为-2,且AB=BC
a,点C表示的数为-2,且AB=BC
![]()
![]() a-(-2a)=-2-(
a-(-2a)=-2-(![]() a)
a)
解得,a=3,
即a的值是3;
(2)由(1)知,a=2,
则BC=﹣2﹣(![]() ×3)=2,
×3)=2,
故等边三角形BCD向右滚动1周得到新的等边三角形BCD,此时点C对应的数为:﹣2+6=4,
∵滚动第n周后,等边三角形BCD的顶点C表示的数是2014,
∴-2+6n=2014,
解得,n=336,
即n的值是336.


科目:初中数学 来源: 题型:
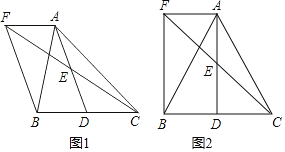
【题目】如图1,在△ABC中,D是BC边上一点,E是AD的中点,过点A作BC的平行线交CE的延长线于F,且AF=BD,连接BF.
(1)求证:点D是线段BC的中点;
(2)如图2,若AB=AC=13,AF=BD=5,求四边形AFBD的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】数学兴趣小组测量校园内旗杆的高度,有以下两种方案:
方案一:小明在地面上直立一根标杆![]() ,沿着直线
,沿着直线![]() 后退到点
后退到点![]() ,使眼睛
,使眼睛![]() 、标杆的顶点
、标杆的顶点![]() 、旗杆的顶点
、旗杆的顶点![]() 在同一直线上(如图1).测量:人与标杆的距离
在同一直线上(如图1).测量:人与标杆的距离![]() =1 m,人与旗杆的距离
=1 m,人与旗杆的距离![]() =16m,人的目高和标杆的高度差
=16m,人的目高和标杆的高度差![]() =0.9m,人的高度
=0.9m,人的高度![]() =1.6m.
=1.6m.
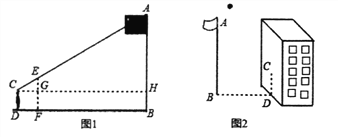
方案二:小聪在某一时刻测得1米长的竹竿竖直放置时影长1.5米,在同时刻测量旗杆的影长时,因旗杆靠近一楼房,影子不全落在地面上,有一部分落在墙上,他测得落在地面上影长为21米,留在墙上的影高为2米(如图2).
请你结合上述两个方案,选择其中的一个方案求旗杆的高度。我选择方案 .
查看答案和解析>>
科目:初中数学 来源: 题型:
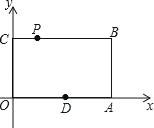
【题目】如图,在平面直角坐标系中,矩形OABC的顶点A、C的坐标分别为(6,0)、(0,4),点P是线段BC上的动点,当△OPA是等腰三角形时,则P点的坐标是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:A(0,1),B(2,0),C(4,3)
(1)在直角坐标系中描出各点,画出△ABC.
(2)求△ABC的面积;
(3)设点P在坐标轴上,且△ABP与△ABC的面积相等,求点P的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知 A=2 x2+3xy﹣2x﹣1,B= x2﹣xy﹣1.
(1)化简:4A﹣(2B+3A),将结果用含有 x、y 的式子表示;
(2)若式子 4A﹣(2B+3A)的值与字母 x 的取值无关,求 y3+![]() A﹣
A﹣ ![]() B 的值.
B 的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,以扇形OAB的顶点O为原点,半径OB所在的直线为x轴,建立平面直角坐标系,点B的坐标为(2,0),若抛物线y= ![]() x2+k与扇形OAB的边界总有两个公共点,则实数k的取值范围是 .
x2+k与扇形OAB的边界总有两个公共点,则实数k的取值范围是 . 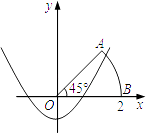
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平整的地面上,有若干个完全相同的棱长为1cm的小正方体堆成一个几何体,如图所示:
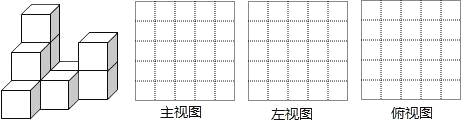
(1)这个几何体是由 个小正方体组成,请画出这个几何体的三视图;
(2)如果在这个几何体露在外面的表面喷上黄色的漆,每平方米用2克,则共需 克漆;
(3)若现在你手头还有一些相同的小正方体,如果保持俯视图和左视图不变,最多可以再添加________个小正方体.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com