
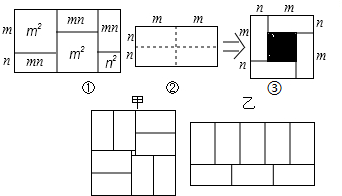
分析 (1)阴影部分的正方形的边长为m-n;
(2)方法①:阴影部分的面积=大正方形的面积-4个小长方形的面积;方法②:表示出小正方形的边长为m-n,即可解答;
(3)大正方形的面积减去4个小长方形的面积即可得出阴影部分的面积,也可得出三个代数式(m+n)2、(m-n)2、mn之间的等量关系;
(4)根据(3)所得出的关系式,可求出(x-y)2的值;
(5)利用图形面积之间关系得出(a+2b)2-8ab=(a-2b)2即可求出.
解答 解:(1)阴影部分的正方形的边长为m-n;
故答案为:m-n.
(2)方法①:阴影部分的面积=大正方形的面积-4个小长方形的面积,
所以阴影部分的面积为:(m+n)2-4mn;
方法②:表示出小正方形的边长为m-n,
所以阴影部分的面积=(m-n)2.
故答案为:(m+n)2-4mn;(m-n)2.
(3)(m-n)2=(m+n)2-4mn;
故答案为:(m-n)2=(m+n)2-4mn.
(4)(x-y)2=(x+y)2-4xy=72-4×10=9;
故答案为:9.
(5)∵(a+2b)2-8ab=(a-2b)2=22=4(cm2),
∴(a+2b)2-8ab的值为4cm2.
故答案为:4cm2.
点评 本题考查了完全平方公式的几何背景,属于基础题,注意仔细观察图形,表示出各图形的面积是关键.


 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案科目:初中数学 来源: 题型:选择题
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 0个 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1组 | B. | 2组 | C. | 3组 | D. | 4组 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
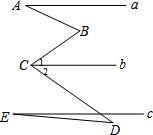 如图,a∥b∥c,∠A=25°,∠1=35°,∠2=45°,∠E=15°,则∠ABC与∠CDE的度数分别为( )
如图,a∥b∥c,∠A=25°,∠1=35°,∠2=45°,∠E=15°,则∠ABC与∠CDE的度数分别为( )| A. | 50°,30° | B. | 60°,30° | C. | 50°,20° | D. | 60°,20° |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com