
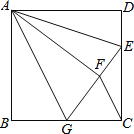
【题目】如图,正方形ABCD中,AB=6,点E在边CD上,且CD=3DE.将△ADE沿AE对折至△AFE,延长EF交边BC于点G,连接AG、CF.则下列结论:①△ABG≌△AFG;②BG=CG;③AG∥CF;④S△EGC=S△AFE;⑤∠AGB+∠AED=145°.其中正确的个数是( )
A. 2 B. 3 C. 4 D. 5
【答案】C
【解析】试题分析:解:①正确.
理由:
∵AB=AD=AF,AG=AG,∠B=∠AFG=90°,
∴Rt△ABG≌Rt△AFG(HL);
②正确.
理由:
EF=DE=![]() CD=2,设BG=FG=x,则CG=6﹣x.
CD=2,设BG=FG=x,则CG=6﹣x.
在直角△ECG中,根据勾股定理,得(6﹣x)2+42=(x+2)2,
解得x=3.
∴BG=3=6﹣3=GC;
③正确.
理由:
∵CG=BG,BG=GF,
∴CG=GF,
∴△FGC是等腰三角形,∠GFC=∠GCF.
又∵Rt△ABG≌Rt△AFG;
∴∠AGB=∠AGF,∠AGB+∠AGF=2∠AGB=180°﹣∠FGC=∠GFC+∠GCF=2∠GFC=2∠GCF,
∴∠AGB=∠AGF=∠GFC=∠GCF,
∴AG∥CF;
④正确.
理由:
∵S△GCE=![]() GCCE=
GCCE=![]() ×3×4=6,
×3×4=6,
∵S△AFE=![]() AFEF=
AFEF=![]() ×6×2=6,
×6×2=6,
∴S△EGC=S△AFE;
⑤错误.
∵∠BAG=∠FAG,∠DAE=∠FAE,
又∵∠BAD=90°,
∴∠GAF=45°,
∴∠AGB+∠AED=180°﹣∠GAF=135°.
故选:C.


 英才计划期末调研系列答案
英才计划期末调研系列答案科目:初中数学 来源: 题型:
【题目】已知![]() 是
是![]() 的直径,
的直径,![]() ,
,![]() 、
、![]() 分别与圆相交于
分别与圆相交于![]() 、
、![]() ,那么下列等式中一定成立的是( )
,那么下列等式中一定成立的是( )
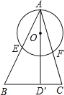
A. AEBF=AFCF B. AEAB=AOAD'
C. AEAB=AFAC D. AEAF=AOAD
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB为⊙O的直径,C是⊙O上一点,过点C的直线交AB的延长线于点D,AE⊥DC,垂足为E,F是AE与⊙O的交点,AC平分∠BAE.

(1)求证:DE是⊙O的切线;
(2)若AE=6,∠D=30°,求图中阴影部分的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:□ABCD的两边AB,AD的长是关于x的方程x2-mx+![]() -
-![]() =0的两个实数根.
=0的两个实数根.
(1)当m为何值时,四边形ABCD是菱形?求出这时菱形的边长;
(2)若AB的长为2,那么□ABCD的周长是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】用配方法解下列方程时,配方有错误的是( )
A.x2﹣2x﹣99=0化为(x﹣1)2=100
B.x2+8x+9=0化为(x+4)2=25
C.2t2﹣7t﹣4=0化为(t﹣![]() )2=
)2=![]()
D.3x2﹣4x﹣2=0化为(x﹣![]() )2=
)2=![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
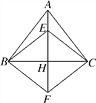
【题目】如图,在等腰三角形ABC中,AB=AC,AH⊥BC,点E是AH上一点,延长AH至点F,使FH=EH.
(1)求证:四边形EBFC是菱形;
(2)如果∠BAC=∠ECF,求证:AC⊥CF.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】观察下列4个命题:其中真命题是( )
(1)三角形的外角和是180°;(2)三角形的三个内角中至少有两个锐角;
(3)如果![]() <0,那么y<0;(4)直线a、b、c,如果a⊥b、b⊥c,那么a⊥c.
<0,那么y<0;(4)直线a、b、c,如果a⊥b、b⊥c,那么a⊥c.
A. (1)(2) B. (2)(3) C. (2)(4) D. (3)(4)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某体育休闲超市购进一种成本为![]() 元/个的风筝,据市场调查分析,若按
元/个的风筝,据市场调查分析,若按![]() 元/个销售,一个月能售出
元/个销售,一个月能售出![]() 个,在此基础上,售价每涨
个,在此基础上,售价每涨![]() 元/个,月销售量就减少
元/个,月销售量就减少![]() 个.设这种风筝的销售单价为
个.设这种风筝的销售单价为![]() (元/个),该超市每月销售这种风筝的所获得的利润为
(元/个),该超市每月销售这种风筝的所获得的利润为![]() (元),针对这种风筝的销售情况,请解答下列问题:
(元),针对这种风筝的销售情况,请解答下列问题:
![]() 用含
用含![]() 的代数式分别表示出每个风筝的销售利润为________元,每月卖出的风筝的个数是________个;
的代数式分别表示出每个风筝的销售利润为________元,每月卖出的风筝的个数是________个;
![]() 求
求![]() 与
与![]() 之间的函数关系式;
之间的函数关系式;
![]() 若该超市想在每月销售这种风筝的成本不超过
若该超市想在每月销售这种风筝的成本不超过![]() 元的情况下,使得月销售利润达到
元的情况下,使得月销售利润达到![]() 元,则每个风筝的售价应定为多少元?
元,则每个风筝的售价应定为多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,弹性小球从P(2,0)出发,沿所示方向运动,每当小球碰到正方形OABC的边时反弹,反弹时反射角等于入射角,当小球第一次碰到正方形的边时的点为P1,第二次碰到正方形的边时的点为P2…,第n次碰到正方形的边时的点为Pn,则P2020的坐标是( )
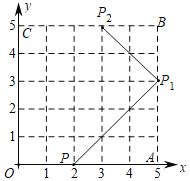
A.(5,3)B.(3,5)C.(0,2)D.(2,0)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com