
分析 (1)首先计算乘方,然后利用同底数的幂的乘法法则即可求得;
(2)首先利用完全平方公式和平方差公式计算,然后合并同类项即可求解;
(3)利用多项式和单项式的除法法则计算即可;
(4)首先对括号内的分式通分相加,然后计算乘方,把除法转化为乘法,最后进行加法运算即可.
解答 解:(1)原式=-a2•a5•a3=-a10;
(2)原式=a2+4ab+4b2-(a2-4b2)-4ab=a2+4ab+4b2-a2+4b2-4ab=8b2;
(3)原式=$\frac{1}{3}$x2+2xy-$\frac{1}{3}$y;
(4)原式=1-$【\frac{a(a-1)+1}{a-1}{】}^{2}$•$\frac{(a-1)^{2}}{{a}^{2}-a+1}$
=1-$\frac{({a}^{2}-a+1)^{2}}{(a-1)^{2}}$•$\frac{(a-1)^{2}}{{a}^{2}-a+1}$
=1-(a2-a+1)
=-a2+a.
点评 本题主要考查了整式的混合运算和分式的混合运算,理解完全平方公式和平方差公式的运用,熟记公式是解题的关键.


科目:初中数学 来源: 题型:填空题
 如图是小明在建筑物AB上用激光仪测量另一建筑物CD高度的示意图,在地面点P处水平放置一平面镜,一束激光从点A射出经平面镜上的点P反射后刚好射到建筑物CD的顶端C处,已知AB⊥BD,CD⊥BD,且测得AB=15米,BP=20米,PD=32米,B、P、D在一条直线上,那么建筑物CD的高度是24米.
如图是小明在建筑物AB上用激光仪测量另一建筑物CD高度的示意图,在地面点P处水平放置一平面镜,一束激光从点A射出经平面镜上的点P反射后刚好射到建筑物CD的顶端C处,已知AB⊥BD,CD⊥BD,且测得AB=15米,BP=20米,PD=32米,B、P、D在一条直线上,那么建筑物CD的高度是24米.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | x=-$\frac{764}{179}$ | B. | x=$\frac{764}{179}$ | C. | x=-$\frac{765}{179}$ | D. | x=$\frac{765}{179}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
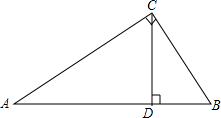 如图,在Rt△ABC中,∠C=90°,CD是斜边AB上的高,下列线段的比值不等于cosA的值的是( )
如图,在Rt△ABC中,∠C=90°,CD是斜边AB上的高,下列线段的比值不等于cosA的值的是( )| A. | $\frac{AD}{AC}$ | B. | $\frac{AC}{AB}$ | C. | $\frac{BD}{BC}$ | D. | $\frac{CD}{BC}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
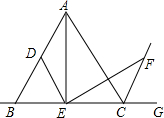 如图,△ABC是等边三角形,∠AEF=60°,ED∥AC交AB于点D,EF,交等边三角形外角平分线CF所在的直线与点F,当点E是BC的中点时,求证:AE=EF.
如图,△ABC是等边三角形,∠AEF=60°,ED∥AC交AB于点D,EF,交等边三角形外角平分线CF所在的直线与点F,当点E是BC的中点时,求证:AE=EF.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com