
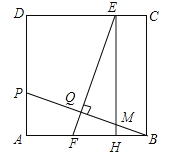
【题目】如图,在正方形ABCD中,点P在AD上,且不与A、D重合,BP的垂直平分线分别交CD、AB于E、F两点,垂足为Q,过E作EH⊥AB于H.
(1)求证:HF=AP;
(2)若正方形ABCD的边长为12,AP=4,求线段EQ的长.
【答案】(1)证明见试题解析;(2)![]() .
.
【解析】
试题分析:(1)由EQ⊥BO,EH⊥AB得到∠EQN=∠BHM=90°,由∠EMQ=∠BMH得到△EMQ∽△BMH,故∠QEM=∠HBM.由ASA定理得到△APB≌△HFE,故可得出结论;
(2)根据勾股定理求出BP的长,由EF是BP的垂直平分线可知BQ=![]() BP,再由锐角三角函数的定义得出QF=BQ的长,由(1)知,△APB≌△HFE,故EF=BP=
BP,再由锐角三角函数的定义得出QF=BQ的长,由(1)知,△APB≌△HFE,故EF=BP=![]() ,再由EQ=EF﹣QF即可得出结论.
,再由EQ=EF﹣QF即可得出结论.
试题解析:(1)∵EQ⊥BO,EH⊥AB,∴∠EQN=∠BHM=90°,∵∠EMQ=∠BMH,∴△EMQ∽△BMH,∴∠QEM=∠HBM,在Rt△APB与Rt△HFE中,∵∠QEM=∠HBM,∠PAB=∠FHE,AB=EH,∴△APB≌△HFE,∴HF=AP;
(2)由勾股定理得,BP=![]() =
=![]() =4
=4![]() ,∵EF是BP的垂直平分线,∴BQ=
,∵EF是BP的垂直平分线,∴BQ=![]() BP=
BP=![]() ,∴QF=BQtan∠FBQ=BQtan∠ABP=
,∴QF=BQtan∠FBQ=BQtan∠ABP=![]() =
=![]() ,由(1)知,△APB≌△HFE,∴EF=BP=
,由(1)知,△APB≌△HFE,∴EF=BP=![]() ,∴EQ=EF﹣QF=
,∴EQ=EF﹣QF=![]() =
=![]() .
.


 轻巧夺冠周测月考直通中考系列答案
轻巧夺冠周测月考直通中考系列答案科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,对角线AC,BD相交于点O,且AC⊥BD,点E,F,G,H分别是AB,BC,CD,DA的中点,依次连接各边中点得到四边形EFGH,求证:四边形EFGH是矩形. 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,边长为1的菱形ABCD中,∠DAB=60°,连接对角线AC,以AC为边作第二个菱形ACEF,使∠FAC=60°,连接AE,再以AE为边作第三个菱形AEGH,使∠HAE=60°,按此规律下去,则第n个菱形的边长为 . 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知四边形ABCD和四边形DEFG为正方形,点E在线段DE上,点A,D,G在同一直线上,且AD=3,DE=1,连接AC,CG,AE,并延长AE交CG于点H.
(1)求sin∠EAC的值.
(2)求线段AH的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD的对角线AC,BD相交于点O,延长CB至点F,使CF=CA,连接AF,∠ACF的平分线分别交AF,AB,BD于点E,N,M,连接EO.
(1)已知BD=![]() ,求正方形ABCD的边长;
,求正方形ABCD的边长;
(2)猜想线段EM与CN的数量关系并加以证明.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,OA⊥OC,OB⊥OD,下面结论:①∠AOB=∠COD;②∠AOB+∠COD=90°;③∠BOC+∠AOD=180°;④∠AOC﹣∠COD=∠BOC中,正确的有(填序号).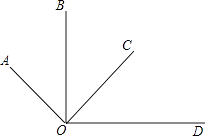
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某汽车队运送一批货物,若每辆车装4吨,还剩下8吨未装;若每辆车装4.5吨,不仅装完全部货物,并且其中有一辆车只装了3.5吨。这个汽车队共派了多少辆汽车运输这批货物?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com