
【题目】如图,正方形ABCD的对角线AC,BD相交于点O,延长CB至点F,使CF=CA,连接AF,∠ACF的平分线分别交AF,AB,BD于点E,N,M,连接EO.
(1)已知BD=![]() ,求正方形ABCD的边长;
,求正方形ABCD的边长;
(2)猜想线段EM与CN的数量关系并加以证明.

【答案】(1)1;(2)CN=![]() CM.
CM.
【解析】
试题分析:(1)根据正方形的性质以及勾股定理即可求得;
(2)根据等腰三角形三线合一的性质证得CE⊥AF,进一步得出∠BAF=∠BCN,然后通过证得△ABF≌△CBN得出AF=CN,进而证得△ABF∽△COM,根据相似三角形的性质和正方形的性质即可证得CN=![]() CM.
CM.
试题解析:(1)∵四边形ABCD是正方形,∴△ABD是等腰直角三角形,∴2AB2=BD2,∵BD=![]() ,∴AB=1,∴正方形ABCD的边长为1;
,∴AB=1,∴正方形ABCD的边长为1;
(2)CN=![]() CM.
CM.
证明:∵CF=CA,AF是∠ACF的平分线,∴CE⊥AF,∴∠AEN=∠CBN=90°,∵∠ANE=∠CNB,∴∠BAF=∠BCN,在△ABF和△CBN中,∵∠BAF=∠BCN,∠ABF=∠CBN,AB=BC,∴△ABF≌△CBN(AAS),∴AF=CN,∵∠BAF=∠BCN,∠ACN=∠BCN,∴∠BAF=∠OCM,∵四边形ABCD是正方形,∴AC⊥BD,∴∠ABF=∠COM=90°,∴△ABF∽△COM,∴![]() ,∴
,∴![]() ,即CN=
,即CN=![]() CM.
CM.


科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠A=90°,AB=AC,BC=20,DE是△ABC的中位线,点M是边BC上一点,BM=3,点N是线段MC上的一个动点,连接DN,ME,DN与ME相交于点O.若△OMN是直角三角形,则DO的长是 . 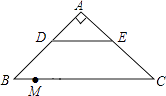
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,正方形ABCD的位置如图所示,点A的坐标为(1,0),点D的坐标为(0,2).延长CB交x轴于点A1,作第1个正方形A1B1C1C;延长C1B1交x轴于点A2,作第2个正方形A2B2C2C1,…,按这样的规律进行下去,第2016个正方形的面积是 .
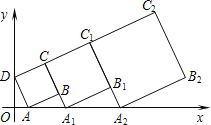
查看答案和解析>>
科目:初中数学 来源: 题型:
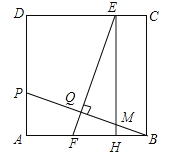
【题目】如图,在正方形ABCD中,点P在AD上,且不与A、D重合,BP的垂直平分线分别交CD、AB于E、F两点,垂足为Q,过E作EH⊥AB于H.
(1)求证:HF=AP;
(2)若正方形ABCD的边长为12,AP=4,求线段EQ的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图.△ABC中,AB=AC,AB的垂直平分线交AC于P点,若AB=6cm,BC=4cm,△PBC的周长等于( ) 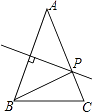
A.4cm
B.6cm
C.8cm
D.10cm
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC和△DEC中,已知AB=DE,还需添加两个条件才能使△ABC≌△DEC,不能添加的一组条件是( ) 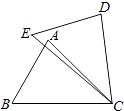
A.BC=EC,∠B=∠E
B.BC=EC,AC=DC
C.BC=DC,∠A=∠D
D.∠B=∠E,∠A=∠D
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】乘法公式的探究与应用: 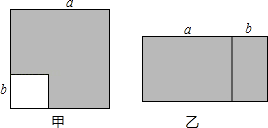
(1)如图甲,边长为a的大正方形中有一个边长为b的小正方形,请你写出阴影部分面积是(写成两数平方差的形式)
(2)小颖将阴影部分裁下来,重新拼成一个长方形,如图乙,则长方形的长是 , 宽是 , 面积是(写成多项式乘法的形式).
(3)比较甲乙两图阴影部分的面积,可以得到公式(两个) 公式1:
公式2:
(4)运用你所得到的公式计算:10.3×9.7.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com