
【题目】学校准备在各班设立图书角以丰富同学们的课余文化生活,为了更合理的搭配各类书籍,学校团委以“我最喜爱的书籍”为主题,对学生最喜爱的一种书籍类型进行随机抽样调查,收集整理数据后,绘制出以下两幅未完成的统计图,请根据图1和图2提供的信息,解答下列问题:


(1)在这次抽样调查中,一共调查了多少名学生?
(2)请把折线统计图(图1)补充完整;
(3)求出扇形统计图(图2)中,体育部分所对应的圆心角的度数;
(4)如果这所中学共有学生1800名,那么请你估计最喜爱科普类书籍的学生人数.
(5)学校若在喜爱艺术、文学、科普、体育四类中任意抽取两类建立兴趣小组,求出恰好选中是体育和科普两类的概率?
【答案】(1)300人. (2)补图见解析;(3)![]() ; (4)480人;(5)
; (4)480人;(5)![]() .
.
【解析】试题分析:
(1)由折线图知喜爱文学的人数,由扇形统计图可知喜爱文学学生所占的百分比,则此则可求出参加调查学生的总数;
(2)结合折线图与扇形图计算出喜爱艺术的人数和其他的人数;
(3)用喜爱体育学生点总人数的百分比乘以360°;
(4)用样本估计总体,通过300个中喜爱科普类书籍估计结果;
(5)这是一个等可能事件,画出树状图,列出所有可能的结果,是科普和体育的结果,从而计算出是体育和科普两类的概率.
试题解析:
(1)调查的学生人数为:90÷30%=300人.
(2)如图
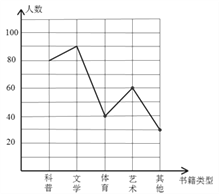
(3)喜爱体育书籍的学生人数为: 300―80―90―60―30=40.
体育部分所对的圆心角为: ![]() .
.
(4)在抽样调查中,喜欢科普类书籍所占比例为: ![]() ,可以估计,在全校同学中,喜欢科普类书籍的人数大约占了
,可以估计,在全校同学中,喜欢科普类书籍的人数大约占了![]() , 人数约为1800×
, 人数约为1800×![]() =480人.
=480人.
(5)画出树状图:
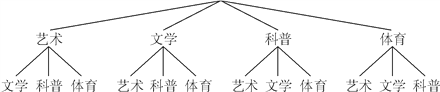
∴P(选中恰是体育和科普)=![]() .
.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】一个不透明的口袋中装有4个完全相同的小球,分别标有数字1,2,3,4,另外有一个可以自由旋转的圆盘,被分成面积相等的3个扇形区域,分别标有数字1,2,3(如图所示).

(1)从口袋中摸出一个小球,所摸球上的数字大于2的概率为 ;
(2)小龙和小东想通过游戏来决定谁代表学校参加歌咏比赛,游戏规则为:一人从口袋中摸出一个小球,另一人转动圆盘,如果所摸球上的数字与圆盘上转出数字之和小于5,那么小龙去;否则小东去.你认为游戏公平吗?请用树状图或列表法说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们对平面直角坐标系 ![]() 中的三角形给出新的定义:三角形的“横长”和三角形的“纵长”.我们假设点
中的三角形给出新的定义:三角形的“横长”和三角形的“纵长”.我们假设点 ![]() ,
, ![]() 是三角形边上的任意两点.如果
是三角形边上的任意两点.如果 ![]() 的最大值为
的最大值为 ![]() ,那么三角形的“横长”
,那么三角形的“横长” ![]() ;如果
;如果 ![]() 的最大值为
的最大值为 ![]() ,那么三角形的“纵长”
,那么三角形的“纵长” ![]() .如右图,该三角形的“横长”
.如右图,该三角形的“横长” ![]() ;“纵长”
;“纵长” ![]() .
.
当 ![]() 时,我们管这样的三角形叫做“方三角形”.
时,我们管这样的三角形叫做“方三角形”.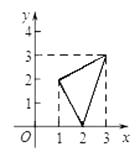
(1)如图1所示,
已知点 ![]() ,
, ![]() .
.
在点 ![]() ,
, ![]() ,
, ![]() 中,可以和点
中,可以和点 ![]() ,点
,点 ![]() 构成“方三角形”的点是;
构成“方三角形”的点是;
(2)若点 ![]() 在函数
在函数 ![]() 上,且
上,且 ![]() 为“方三角形”,求点
为“方三角形”,求点 ![]() 的坐标;
的坐标;
(3)如图2所示,已知点 ![]() ,
, ![]() ,点
,点 ![]() 为平面直角坐标系中任意一点.若
为平面直角坐标系中任意一点.若 ![]() 为“方三角形”,且
为“方三角形”,且 ![]() ,请直接写出点
,请直接写出点 ![]() 的坐标.
的坐标.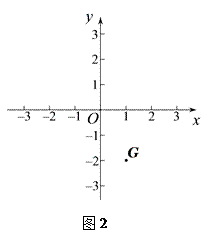
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】抛物线C1:y=x2+1与抛物线C2关于X轴对称,则抛物线C2的解析式为( )
A. y=-x2 B. y=-x2+1 C. y=x2-1 D. y=-x2-1
查看答案和解析>>
科目:初中数学 来源: 题型:
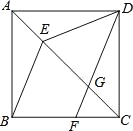
【题目】如图,在正方形ABCD中,点E在对角线AC上,点F在边BC上,连接BE、DF,DF交对角线AC于点G,且DE=DG.
(1)求证:AE=CG;
(2)试判断BE和DF的位置关系,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】保护环境,让我们从垃圾分类做起.某区环保部门为了提高宣传实效,抽样调查了部分居民小区一段时间内生活垃圾的分类情况(如图1),进行整理后,绘制了如下两幅尚不完整的统计图: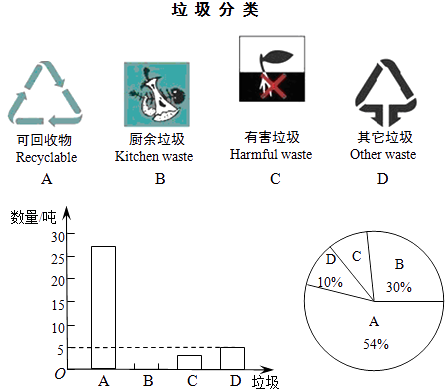
根据图表解答下列问题:
(1)请将图2﹣条形统计图补充完整;
(2)在图3﹣扇形统计图中,求出“D”部分所对应的圆心角等于度;
(3)在抽样数据中,产生的有害垃圾共有吨;
(4)调查发现,在可回收物中废纸垃圾约占 ![]() ,若每回收1吨废纸可再造好纸0.85吨.假设该城市每月产生的生活垃圾为10000吨,且全部分类处理,那么每月回收的废纸可再造好纸多少吨?
,若每回收1吨废纸可再造好纸0.85吨.假设该城市每月产生的生活垃圾为10000吨,且全部分类处理,那么每月回收的废纸可再造好纸多少吨?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,线段 AB上的点数与线段的总数有如下关系:如果线段上有3个点时,线段共有3条;如果线段上有4个点时,线段共有6条;如果线段上有5个点时,线段共有10条;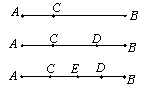
(1)当线段上有6个点时,线段共有条?
(2)当线段上有n个点时,线段共有多少条?(用n的代数式表示)
(3)当n=100时,线段共有多少条?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com