
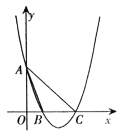
【题目】如图,抛物线![]() 交
交![]() 轴于
轴于![]() ,
,![]() 两点,交
两点,交![]() 轴于
轴于![]() 点,连接
点,连接![]() ,点
,点![]() 为抛物线上一动点.
为抛物线上一动点.
(1)求抛物线的解析式;
(2)当点![]() 到直线
到直线![]() 的距离为
的距离为![]() 时,求点
时,求点![]() 的横坐标;
的横坐标;
(3)当![]() 和
和![]() 的面积相等时,请直接写出点
的面积相等时,请直接写出点![]() 的坐标.
的坐标.
【答案】(1)![]() ;(2)点
;(2)点![]() 的横坐标为
的横坐标为![]() 或
或![]() ;(3)
;(3)![]() 或
或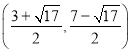 或
或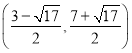
【解析】
(1)把![]() ,
,![]() 代入解析式即可求解; (2)过P作
代入解析式即可求解; (2)过P作![]() ,
,![]() 轴交AB于D,构建直角三角形,利用三角函数建立
轴交AB于D,构建直角三角形,利用三角函数建立![]() 与PD的关系即可求解; (3)△ACP和△ABC的面积相等,过
与PD的关系即可求解; (3)△ACP和△ABC的面积相等,过![]() 作
作![]() 的平行线与抛物线的交点符合题意,再把
的平行线与抛物线的交点符合题意,再把![]() 向上平移两平行线间的距离得另两个交点也符合题意,联立两个解析式即可求解.
向上平移两平行线间的距离得另两个交点也符合题意,联立两个解析式即可求解.
解:(1)把![]() ,
,![]() 代入
代入![]() 得
得
![]()
解得:![]()
所以,抛物线的解析式为:![]()
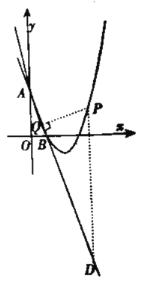
(2)过点![]() 作
作![]() 于
于![]() ,过点
,过点![]() 作
作![]() 轴交直线
轴交直线![]() 于
于![]() ,
,
则![]() ,
,
![]() ,
,![]()
![]() ,
,![]() ,
,
![]() 直线
直线![]() 的解析式为:
的解析式为:![]()
![]()
![]()
又![]()
![]()
![]()
设点![]() ,
,![]()
![]() ,
,![]()
![]() ,
,![]() ,
,
当![]() 时,解得:
时,解得:![]() ,
,![]()
当![]() ,方程无解.
,方程无解.
故点![]() 的横坐标为
的横坐标为![]() 或
或![]()
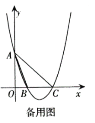
(3)如图,
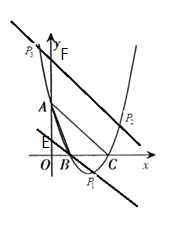
过B作![]() ,则
,则![]() ,
,
![]() ,
,![]() ,
,
所以设 ![]() 为
为![]() ,把
,把![]() 代入得,
代入得,![]() ,
,
所以![]() :
:![]()
所以![]() 解得:
解得:![]() ,
,
所以![]() .
.
因为![]() :
:![]() ,所以
,所以![]() ,又
,又![]() ,
,
所以![]() ,把
,把![]() 向上平移4个单位长度得:
向上平移4个单位长度得:![]() ,
,
所以 ![]() ,解得:
,解得: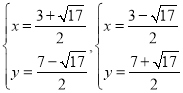 ,
,
所以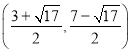 ,
,![]()
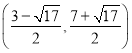
所以P的坐标为![]() 或
或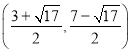 或
或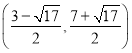


科目:初中数学 来源: 题型:
【题目】工人师傅用一块长为10dm,宽为6dm的矩形铁皮制作一个无盖的长方体容器,需要将四角各裁掉一个正方形.(厚度不计)

(1)在图中画出裁剪示意图,用实线表示裁剪线,虚线表示折痕;并求长方体底面面积为12dm2时,裁掉的正方形边长多大?
(2)若要求制作的长方体的底面长不大于底面宽的五倍,并将容器进行防锈处理,侧面每平方分米的费用为0.5元,底面每平方分米的费用为2元,裁掉的正方形边长多大时,总费用最低,最低为多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,⊙O的半径为1,点A在x轴的正半轴上,B为⊙O上一点,过点A、B的直线与y轴交于点C,且OA2=ABAC.

(1)求证:直线AB是⊙O的切线;
(2)若AB=![]() ,求直线AB对应的函数表达式.
,求直线AB对应的函数表达式.
查看答案和解析>>
科目:初中数学 来源: 题型:
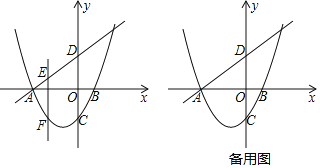
【题目】如图,抛物线y=ax2+bx﹣1(a≠0)交x轴于A,B(1,0)两点,交y轴于点C,一次函数y=x+3的图象交坐标轴于A,D两点,E为直线AD上一点,作EF⊥x轴,交抛物线于点F
(1)求抛物线的解析式;
(2)若点F位于直线AD的下方,请问线段EF是否有最大值?若有,求出最大值并求出点E的坐标;若没有,请说明理由;
(3)在平面直角坐标系内存在点G,使得G,E,D,C为顶点的四边形为菱形,请直接写出点G的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,![]() 为
为![]() 的直径,
的直径,![]() 于
于![]() ,点
,点![]() 是弧
是弧![]() 上的任一点,过点
上的任一点,过点![]() 作
作![]() 的切线交
的切线交![]() 于点
于点![]() .连接
.连接![]() 交
交![]() 于
于![]() .
.
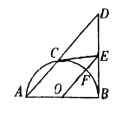
(1)求证:![]() ;
;
(2)填空:①当![]() _____时,四边形
_____时,四边形![]() 是正方形;
是正方形;
②当![]() _____时,四边形
_____时,四边形![]() 是菱形.
是菱形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,以点A为中心,把△ABC逆时针旋转120°,得到△AB'C′(点B、C的对应点分别为点B′、C′),连接BB',若AC'∥BB',则∠CAB'的度数为( )

A.45°B.60°C.70°D.90°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知A(-4,n)、B(3,4)是一次函数y1=kx+b的图象与反比例函数![]() 的图象的两个交点,过点D(t,0)(0<t<3)作x轴的垂线,分别交双曲线
的图象的两个交点,过点D(t,0)(0<t<3)作x轴的垂线,分别交双曲线![]() 和直线y1=kx+b于P、Q两点
和直线y1=kx+b于P、Q两点
(1) 直接写出反比例函数和一次函数的解析式
(2) 当t为何值时,S△BPQ=![]() S△APQ
S△APQ
(3) 以PQ为边在直线PQ的右侧作正方形PQMN,试说明:边QM与双曲线![]() (x>0)始终有交点
(x>0)始终有交点

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2019年“519(我要走)全国徒步日(江夏站)”暨第六届“环江夏”徒步大会5月19日在美丽的花山脚下降重举行.组委会(活动主办方)为了奖励活动中取得了好成绩的参赛选手,计划购买共100件的甲、乙两种纪念品发放.其中甲种纪念品每件售价120元,乙种纪念品每件售价80元.
(1)如果购买甲、乙两种纪念品一共花费了9600元,求购买甲、乙两种纪念品各是多少件?
(2)设购买甲种纪念品![]() 件,如果购买乙种纪念品的件数不超过甲种纪念品的数量的2倍,并且总费用不超过9400元.问组委会购买甲、乙两种纪念品共有几种方案?哪一种方案所需总费用最少?最少总费用是多少元?
件,如果购买乙种纪念品的件数不超过甲种纪念品的数量的2倍,并且总费用不超过9400元.问组委会购买甲、乙两种纪念品共有几种方案?哪一种方案所需总费用最少?最少总费用是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,∠ACB=90°,D是AB边上一点,以BD为直径的⊙O与边AC有公共点E,连结DE并延长,与BC的延长线交于点F ,BD=BF.
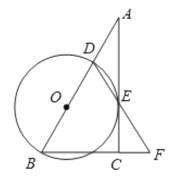
(1)求证:AC是⊙O的切线;
(2)若∠F=60°,BF=8,求CF的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com