
【题目】在△ABC中,∠ACB=90°,D是AB边上一点,以BD为直径的⊙O与边AC有公共点E,连结DE并延长,与BC的延长线交于点F ,BD=BF.
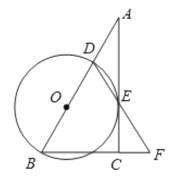
(1)求证:AC是⊙O的切线;
(2)若∠F=60°,BF=8,求CF的长.
【答案】(1)详见解析;(2)CF=2.
【解析】
(1)连接连接BE,OE,根据直径所对的角为直角结合等腰三角形三线合一的性质可证得DE=EF,根据三角形中位线定理可推出OE∥BC,得出OE⊥AC,即可证明结论;
(2)利用三角形中位线定理可求得半径OE的长,利用含30度角的直角三角形的性质可求得OA进而求得AB,即可求得BC的长,从而得解.
(1)连接BE,OE,
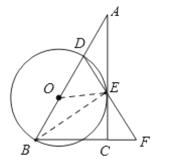
∵BD是直径,
∴∠DEB=90°,
∴BE⊥DF,
∵BD=BF,
∴DE=EF,
又∵DO=OB,
∴OE∥BF,
∵∠ACB=90°,
∴∠OEA=∠ACB =90°,
∴OE⊥AC,
∴AC是圆O的切线;
(2)∵BD=BF,∠F=60°,
∴△DBF为等边三角形,
∴∠ABC=60°,
∴∠A=∠ACB-∠ABC =90°-60°=30°,
∵DE=EF,DO=OB,
∴OE=![]() ,
,
在![]() 中,∠OEA =90°,∠A=30°,
中,∠OEA =90°,∠A=30°,
∴AO=2OE=8,
∴AB= AO +OB= AO +OE= 8 +4=12,
在![]() 中,∠ACB =90°,∠A=30°,
中,∠ACB =90°,∠A=30°,
∴BC=![]() =6,
=6,
∴CF=BF-BC=2.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
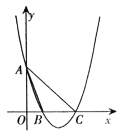
【题目】如图,抛物线![]() 交
交![]() 轴于
轴于![]() ,
,![]() 两点,交
两点,交![]() 轴于
轴于![]() 点,连接
点,连接![]() ,点
,点![]() 为抛物线上一动点.
为抛物线上一动点.
(1)求抛物线的解析式;
(2)当点![]() 到直线
到直线![]() 的距离为
的距离为![]() 时,求点
时,求点![]() 的横坐标;
的横坐标;
(3)当![]() 和
和![]() 的面积相等时,请直接写出点
的面积相等时,请直接写出点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】函数y=![]() 和y=
和y=![]() 在第一象限内的图象如图,点P是y=
在第一象限内的图象如图,点P是y=![]() 的图象上一动点,PC⊥x轴于点C,交y=
的图象上一动点,PC⊥x轴于点C,交y=![]() 的图象于点B.给出如下结论:①△ODB与△OCA的面积相等;②PA与PB始终相等;③四边形PAOB的面积大小不会发生变化;④CA=
的图象于点B.给出如下结论:①△ODB与△OCA的面积相等;②PA与PB始终相等;③四边形PAOB的面积大小不会发生变化;④CA=![]() AP.其中所有正确结论的序号是( )
AP.其中所有正确结论的序号是( )
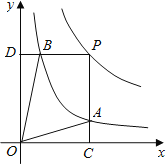
A. ①②③ B. ②③④ C. ①③④ D. ①②④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,以平行四边形ABCD的较短边CD为一边作菱形CDEF,使点F落在边AD上,连接BE,交AF于点G,延长DE,BA交于点H,若∠ADC=60°,则![]() =________
=________
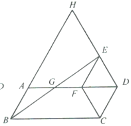
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AD为⊙O直径,作⊙O的内接正三角形ABC,下列作法错误的是( )
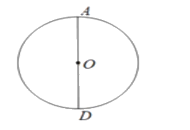
A.作OD的中垂线,交⊙O于B,C,连结AB,AC;
B.以D点为圆心,OD长为半径作圆弧,交圆于点B,C,连结AB, BC,CA;
C.以A点为圆心,AO长为半径作圆弧,交圆于点E,F,再分别以E,F为圆心,AO长为半径作圆弧,交圆于不同于点A的两点B,C,连结AB,BC,CA
D.作AD的中垂线,交⊙O于B,C,连结AB,AC
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读与应用:同学们,你们已经知道![]() ,即
,即![]() .所以
.所以![]() (当且仅当
(当且仅当![]() 时取等号).
时取等号).
阅读1:若![]() 为实数,且
为实数,且![]() (当且仅当
(当且仅当![]() 时取等号).
时取等号).
阅读2:若函数![]() (
(![]() ,
,![]() ,
,![]() 为常数).由阅读1结论可知:
为常数).由阅读1结论可知:![]() 即
即![]() ,∴当
,∴当![]() 即
即![]() 时,函数
时,函数![]() 的最小值为
的最小值为![]() .
.
阅读理解上述内容,解答下列问题:
问题1:若函数![]() ,则
,则![]() = 时,函数
= 时,函数![]() 的最小值为 .
的最小值为 .
问题2:已知一个矩形的面积为4,其中一边长为![]() ,则另一边长为
,则另一边长为![]() ,周长为
,周长为![]() ,求当
,求当![]() 时,矩形周长的最小值为 .
时,矩形周长的最小值为 .
问题3:求代数式![]() 的最小值.
的最小值.
问题4:建造一个容积为8立方米,深2米的长方体无盖水池,池底和池壁的造价分别为每平方米![]() 米,水池总造价为
米,水池总造价为![]() (元),求当
(元),求当![]() 为多少时,水池总造价
为多少时,水池总造价![]() 最低?最低是多少?
最低?最低是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在ABCD中,已知AB=6,BE平分∠ABC交AD边于点E,点E将AD分为1:3两部分,则AD的长为( )
A. 8或24B. 8C. 24D. 9或24
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】![]() 表示以
表示以![]() 为自变量的函数,则
为自变量的函数,则![]() 表示当
表示当![]() 时
时![]() 函数的值.例如,一次函数
函数的值.例如,一次函数![]() 记作
记作![]() ,当
,当![]() 时,函数值
时,函数值![]() .现给出新定义:对于函数
.现给出新定义:对于函数![]() ,若存在实数
,若存在实数![]() ,使得成立
,使得成立![]() ,则称点
,则称点![]() 是函数
是函数![]() 的“奇妙点”.
的“奇妙点”.
(1)求函数![]() 的“奇妙点”;
的“奇妙点”;
(2)当![]() 为何值时,函数
为何值时,函数![]() 存在“奇妙点”?
存在“奇妙点”?
(3)若二次函数![]() 有且只有一个“奇妙点”
有且只有一个“奇妙点”![]() ,其图象与
,其图象与![]() 轴交于
轴交于![]() 两点(点
两点(点![]() 在点
在点![]() 的左侧),
的左侧),![]() 是
是![]() 轴上一动点.当
轴上一动点.当![]() 的周长最短时,求点
的周长最短时,求点![]() 的坐标及
的坐标及![]() 的周长.
的周长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com