
【题目】如图,AD为⊙O直径,作⊙O的内接正三角形ABC,下列作法错误的是( )
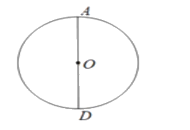
A.作OD的中垂线,交⊙O于B,C,连结AB,AC;
B.以D点为圆心,OD长为半径作圆弧,交圆于点B,C,连结AB, BC,CA;
C.以A点为圆心,AO长为半径作圆弧,交圆于点E,F,再分别以E,F为圆心,AO长为半径作圆弧,交圆于不同于点A的两点B,C,连结AB,BC,CA
D.作AD的中垂线,交⊙O于B,C,连结AB,AC
【答案】D
【解析】
直接利用等边三角形的判定与性质分别分析得出答案.
连接OB、OC,如图1.
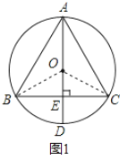
由作图可知:BC是半径OD的垂直平分线,
∵AD为⊙O的直径,
∴![]() ,
,![]() ,
,![]() ,
,
∴AB=AC.
在Rt△OEC中,
∴![]() ,
,
∴∠EOC=60°,
∴∠BOC=120°,
∴∠BAC=60°,
∴△ABC是等边三角形,故A作图正确,不符合题意;
如图2,连接DB、DC.
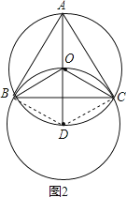
由作图可知:DB=DO=DC,
在⊙O中,OB=OD=OC,
∴△OBD和△OCD都是等边三角形,
∴∠ODB=∠ODC=60°,
∵![]() ,
,
∴∠ODB=∠ACB=∠ABC=∠ODC=60°,
∴△ABC是等边三角形, 故B作图正确,不符合题意;
连接AE,EO,BE,BO,AF,FO,CO,CF,
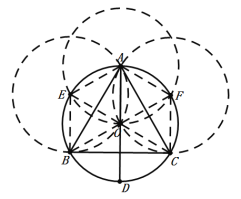
由作图可知:AE=EO=BE=BO=AF=FO=CO=CF=AO,
∴△OAE、△OBE、△OAF、△OCF都是等边三角形,
∴∠AOB=∠AOC=60°+60°=120°,
∴∠BOC=360°-∠AOB=∠AOC=120°,
∵BO =CO =AO,
∴△AOB![]() △AOC
△AOC![]() △BOC,
△BOC,
∴AB=AC=BC,
∴△ABC是等边三角形, 故C作图正确,不符合题意;
由作图可知:OB=OC=OA=OD,
∴△ABC是等腰直角三角形,故D作图错误,符合题意.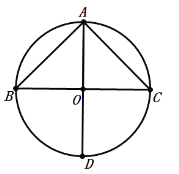
故选:D.


科目:初中数学 来源: 题型:
【题目】如图,![]() 为
为![]() 的直径,
的直径,![]() 于
于![]() ,点
,点![]() 是弧
是弧![]() 上的任一点,过点
上的任一点,过点![]() 作
作![]() 的切线交
的切线交![]() 于点
于点![]() .连接
.连接![]() 交
交![]() 于
于![]() .
.
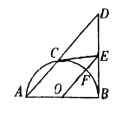
(1)求证:![]() ;
;
(2)填空:①当![]() _____时,四边形
_____时,四边形![]() 是正方形;
是正方形;
②当![]() _____时,四边形
_____时,四边形![]() 是菱形.
是菱形.
查看答案和解析>>
科目:初中数学 来源: 题型:
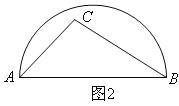
【题目】如图AB是半圆的直径,图1中,点C在半圆外;图2中,点C在半圆内,请仅用无刻度的直尺按要求画图.
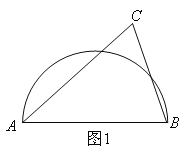
(1)在图1中,画出△ABC的三条高的交点;
(2)在图2中,画出△ABC中AB边上的高.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知函数y=-x2+mx+m+1(其中m为常数)
(1)该函数的图象与X轴公共点的个数是______个
(2)若该函数的图象的对称轴是直线X=1,顶点为点A,求此时函数的解析式及点的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
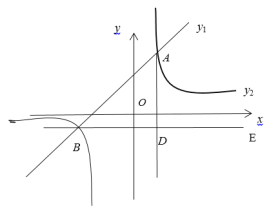
【题目】如图,在平面直角坐标系中,一次函数y1=ax+b的图像与反比例函数![]() 的图像交于点A(2,4)和B(-4,m).
的图像交于点A(2,4)和B(-4,m).
(1)求一次函数和反比例函数的表达式;
(2)过点B做BE//x轴,![]() 于点D,点C是直线BE上一点,若AC=2BC,求点C的坐标.
于点D,点C是直线BE上一点,若AC=2BC,求点C的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,∠ACB=90°,D是AB边上一点,以BD为直径的⊙O与边AC有公共点E,连结DE并延长,与BC的延长线交于点F ,BD=BF.
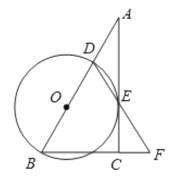
(1)求证:AC是⊙O的切线;
(2)若∠F=60°,BF=8,求CF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,ABCD的对角线AC、BD交于点O,AE平分∠BAD交BC于点E,且∠ADC=60°,AB=![]() BC,连接OE.下列结论:①∠CAD=30°;②SABCD=ABAC;③OB=AB;④OE=
BC,连接OE.下列结论:①∠CAD=30°;②SABCD=ABAC;③OB=AB;④OE=![]() BC,成立的个数有( )
BC,成立的个数有( )

A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校为了了解九年级学生体育测试成绩情况,以九年级(1)班学生的体育测试成绩为样本,按B、C、D四个等级进行统计,并将统计结果绘制如下两幅统计图,请你结合图中所给信息解答下列问题:(说明:A级:90分﹣100分;B级:75分﹣89分;C级:60分~74分;D级:60分以下)
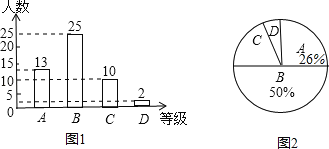
(1)求出D级学生的人数占全班总人数的百分比;
(2)求出扇形统计图(图2)中C级所在的扇形圆心角的度数;
(3)若该校九年级学生共有500人,请你估计这次考试中A级和B级的学生共有多少人?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com