
����Ŀ��![]() ��ʾ��
��ʾ��![]() Ϊ�Ա����ĺ�������
Ϊ�Ա����ĺ�������![]() ��ʾ��
��ʾ��![]() ʱ
ʱ![]() ������ֵ�����磬һ�κ���
������ֵ�����磬һ�κ���![]() ����
����![]() ����
����![]() ʱ������ֵ
ʱ������ֵ![]() ���ָ����¶��壺���ں���
���ָ����¶��壺���ں���![]() ��������ʵ��
��������ʵ��![]() ��ʹ�ó���
��ʹ�ó���![]() ����Ƶ�
����Ƶ�![]() �Ǻ���
�Ǻ���![]() �������������
�������������
��1������![]() �������������
�������������
��2����![]() Ϊ��ֵʱ������
Ϊ��ֵʱ������![]() ���������������
���������������
��3�������κ���![]() ����ֻ��һ�����������
����ֻ��һ�����������![]() ����ͼ����
����ͼ����![]() �ύ��
�ύ��![]() ���㣨��
���㣨��![]() �ڵ�
�ڵ�![]() ����ࣩ��
����ࣩ��![]() ��
��![]() ����һ���㣮��
����һ���㣮��![]() ���ܳ����ʱ�����
���ܳ����ʱ�����![]() �����꼰
�����꼰![]() ���ܳ���
���ܳ���
���𰸡���1��![]() �Ǻ���
�Ǻ���![]() ���������������2��
���������������2��![]() Ϊ����ʵ��ʱ��
Ϊ����ʵ��ʱ��![]() ʱ����3��
ʱ����3��![]() ���ܳ�Ϊ
���ܳ�Ϊ![]() ��
��
��������
��1��������ã�4x+6��2x+12�����x��3����𰸿������
��2�������ֲ�ͬ������ۣ�����2a��2��0����a��1��bΪ����ʵ��ʱ������y��2ax+3b��2��һ��������㡱������2a��2��0��14��3b��0����a��1��b��![]() ʱ������y��2ax+3b��2��������������㡱������2a��2��0��14��3b��0����a��1��b��
ʱ������y��2ax+3b��2��������������㡱������2a��2��0��14��3b��0����a��1��b��![]() ʱ������y��2ax+3b��2û�С�����㡱��
ʱ������y��2ax+3b��2û�С�����㡱��
��3��������÷���ax2��2x+8��2x+12����ֻ��һ���⣬���A�����꣬�ɵö��κ���y����x2��2x+8��ͼ����x��Ľ���ΪB����4��0����C��2��0������ͼ������B����y��ĶԳƵ�B'������B'A��y���ڵ�P����P��Ϊ�������ֱ��B'A�Ľ���ʽΪ![]() �����P���������������AB��AB'�ij����ɵó��𰸣�
�����P���������������AB��AB'�ij����ɵó��𰸣�
�⣺��1��������ã�4x+6��2x+12��
��ã�x��3��
�ࣨ3��18���Ǻ���y��4x+6������㣻
��2����2ax+3b��2��2x+12�ã�2a��2��x��14��3b��
����2a��2��0����a��1��bΪ����ʵ��ʱ�����̣�2a��2��x��14��3b��Ψһ��x��![]() ������y��2ax+3b��2��һ��������㡱��
������y��2ax+3b��2��һ��������㡱��
����2a��2��0��14��3b��0����a��1��b��![]() ʱ�����̣�2a��2��x��14��3b�Ľ�Ϊȫ��ʵ��������y��2ax+3b��2��������������㡱��
ʱ�����̣�2a��2��x��14��3b�Ľ�Ϊȫ��ʵ��������y��2ax+3b��2��������������㡱��
����2a��2��0��14��3b��0����a��1��b��![]() ʱ�����̣�2a��2��x��14��3b�⣬����y��2ax+3b��2û�С�����㡱��
ʱ�����̣�2a��2��x��14��3b�⣬����y��2ax+3b��2û�С�����㡱��
��3���߶��κ���y��ax2��2x+8��a��0������ֻ��һ��������㡱��
���ax2��2x+8��2x+12����ֻ��һ���⣬
�÷��̿ɻ�Ϊax2��4x��4��0��
���������4��2��4������4a����0��
��ã�a����1��
��y����x2��2x+8�ġ�����㡱ΪA����2��8����
����κ����Ľ���ʽΪy����x2��2x+8��
����κ���y����x2��2x+8��ͼ����x��Ľ���ΪB����4��0����C��2��0����
��ͼ������B����y��ĶԳƵ�B'������B'A��y���ڵ�P����P��Ϊ����
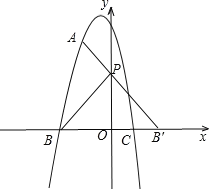
���B'��4��0����
��ֱ��ֱ��B'A�Ľ���ʽΪy��kx+b��
��![]() ��
��
��ã� ��
��
��ֱ��B'A�Ľ���ʽΪ![]() ��
��
��P��0��![]() ����
����
��![]() ��
��![]() ��
��
���PAB���ܳ�Ϊ![]() ��
��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������ABC�У���ACB=90����D��AB����һ�㣬��BDΪֱ������O���AC�й�����E������DE���ӳ�����BC���ӳ��߽��ڵ�F ��BD=BF��
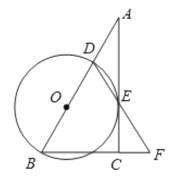
��1����֤��AC����O�����ߣ�
��2������F=60����BF=8����CF�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����꼶��1�����о���ѧϰС��Ϊ�о�ȫУͬѧ�����Ķ��������ȫУ��������˲���ͬѧ�����ʾ����飬ͳ��ͬѧ��һ�����Ķ�������������������������µ�ͳ��ͼ1��ͼ2�������ͼ�������Ϣ������������⣺

����ͼ1��![]() ��ֵΪ____________������____________��ͬѧ�����ʾ����飻
��ֵΪ____________������____________��ͬѧ�����ʾ����飻
������ͳ�Ƶ��������ݵ�ƽ��������������λ����
����ȫУ����ѧ��1500�ˣ������������ݣ����Ƹ�Уѧ��һ�����Ķ�2�������������ԼΪ���٣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪���κ���y ax2 2ax 3a2 3������x���Ա���������x 2ʱ��y��x�������������3 x 0ʱ��y�����ֵΪ9����a��ֵΪ�� ����
A.1��![]() B.
B.![]() ��
��![]() C.
C.![]() D.1
D.1
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪���κ���![]() ��ͼ����ͼ��ʾ���������½��ۣ� ��
��ͼ����ͼ��ʾ���������½��ۣ� ��![]() ����
����![]() ����
���� ![]() ����
����![]() ��������ȷ���۵�����ǣ� ��
��������ȷ���۵�����ǣ� ��
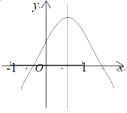
A.�ۢ�B.�ڢ�C.�ڢ�D.�٢ڢ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ֱ��![]() ��Բ
��Բ![]() ��Ϊ������Բ��һ����Բ������һ����
��Ϊ������Բ��һ����Բ������һ����![]() ����һ��Բ������һ����
����һ��Բ������һ����![]() ����
����![]() ��
��![]() ��
��![]() ���ӳ����ڵ�
���ӳ����ڵ�![]() ��
��
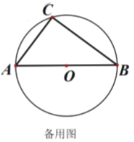
��1����֤��![]()
��2����![]() ��
��![]()
�ٵ���![]() �˶�����Բ��
�˶�����Բ��![]() �е�ʱ����
�е�ʱ����![]() ��
��![]() �ϵĸߣ�
�ϵĸߣ�
�ڵ���![]() �˶���ʲôλ��ʱ��
�˶���ʲôλ��ʱ��![]() �������������������
�������������������![]() ��
��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��![]() �İ뾶Ϊ2����
�İ뾶Ϊ2����![]() ����PΪ�Ż�AB��һ���㣬
����PΪ�Ż�AB��һ���㣬![]() ����ֱ��PB�ڵ�C����
����ֱ��PB�ڵ�C����![]() ����������
����������![]()
![]()
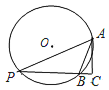
A.![]() B.1C.2D.
B.1C.2D.![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij��Ϊ�˿�չ�����������˶������ƻ����������������֪����ĵ��۱�����ĵ��۶�![]() Ԫ��������
Ԫ��������![]() �������
�������![]() �������軨��
�������軨��![]() Ԫ��
Ԫ��
��1�������������ĵ��۸��Ƕ���Ԫ��
��2����ѧУ�������������![]() �����ҹ���������ܽ���������������ܽ���ѧУ���ɹ�����ٸ�����
�����ҹ���������ܽ���������������ܽ���ѧУ���ɹ�����ٸ�����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
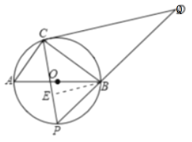
����Ŀ����ͼ��AB�ǡ�O��ֱ����C�ǡ�O��һ�㣬D��![]() ���е㣬EΪOD�ӳ�����һ�㣬�ҡ�CAE=2��C��AC��BD���ڵ�H����OE���ڵ�F��
���е㣬EΪOD�ӳ�����һ�㣬�ҡ�CAE=2��C��AC��BD���ڵ�H����OE���ڵ�F��
(1)��֤��AE�ǡ�O�����ߣ�
(2)��DH=9��tanC=![]() ����ֱ��AB�ij���
����ֱ��AB�ij���
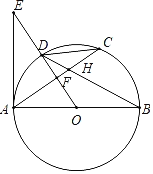
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com