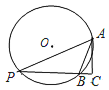
【题目】如图，
的半径为2，弦
，点P为优弧AB上一动点，
，交直线PB于点C，则
的最大面积是
A.
B.1C.2D.
科目：初中数学 来源： 题型：
【题目】阅读与应用：同学们，你们已经知道
，即
．所以
（当且仅当
时取等号）．
阅读1：若
为实数，且
（当且仅当时取等号）．
阅读2：若函数
（
，
，
为常数）．由阅读1结论可知：
即
，∴当
即
时，函数的最小值为
．
阅读理解上述内容，解答下列问题：
问题1：若函数
，则
= 时，函数的最小值为 ．
问题2：已知一个矩形的面积为4，其中一边长为
，则另一边长为
，周长为
，求当
时，矩形周长的最小值为 ．
问题3：求代数式
的最小值．
问题4：建造一个容积为8立方米，深2米的长方体无盖水池，池底和池壁的造价分别为每平方米米，水池总造价为
（元），求当为多少时，水池总造价最低？最低是多少？
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】为了推动阳光体育运动的广泛开展，引导学生走向操场、走进大自然、走到阳光下，积极参加体育锻炼，学校准备购买一批运动鞋供学生借用．现从各年级随机抽取了部分学生的鞋号，绘制出如下的统计图①和图②，请根据相关信息,解答下列问题：
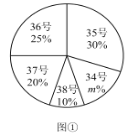
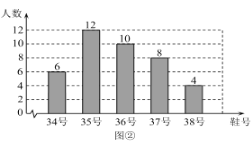
（Ⅰ）本次接受随机抽样调查的学生人数为________，图①中
的值为________；
（Ⅱ）求本次调查获取的样本数据的众数和中位数；
（Ⅲ）根据样本数据，若学校计划购买150双运动鞋,建议购买35号运动鞋多少双？
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】
表示以
为自变量的函数，则
表示当
时
函数的值．例如，一次函数
记作
，当时，函数值
．现给出新定义：对于函数，若存在实数
，使得成立
，则称点
是函数
的“奇妙点”．
（1）求函数
的“奇妙点”；
（2）当
为何值时，函数
存在“奇妙点”？
（3）若二次函数
有且只有一个“奇妙点”
，其图象与轴交于
两点（点
在点
的左侧），
是
轴上一动点．当
的周长最短时，求点的坐标及的周长．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】初三第一轮复习重在查漏补缺，课后很重要的一项任务是“纠错”．在深大附中九年级随机抽取部分学生进行调查，对平时的错题：
表示“每一道错题都解决了”，
表示“大部分错题解决了”，
表示“只有一部分错题解决了”，
表示“从不解决错题”．对抽取的学生问卷统计后如图：
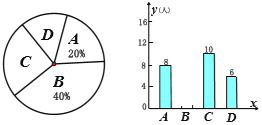
（1）抽查的学生有______人；扇形统计图中，占比_______；占比_______．
（2）补全条形统计图；
（3）全年级有480人，估计对错题“全解决”和“大部分解决”共有多少学生？
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，Rt△ABC中，∠ABC=90°，以AB为直径作⊙O，点D为⊙O上一点，且CD=CB、连接DO并延长交CB的延长线于点E．
（1）判断直线CD与⊙O的位置关系，并说明理由；
（2）若BE=4，DE=8，求AC的长．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在直角坐标系中，已知A(4，4)，B(-1，1)，EF=1，线段EF在x轴上平移，当四边形ABEF的周长最小时，点E坐标是__________．
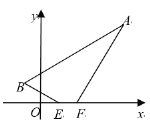
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】某商场销售一种名牌衬衫，平均每天可售出20件，每件盈利40元，为了扩大销售，增加盈利，尽量减少库存，商场决定采取适当的降价措施，经调查发现，如果每件衬衫每降价1元，商场平均每天可多售出2件，
（1）若商场平均每天要盈利1200元，每件衬衫应降价多少元？
（2）当每件衬衫降价多少元时，商场每天获利最大，每天获利最大是多少元？
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
