
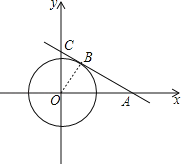
【题目】如图,在平面直角坐标系中,⊙O的半径为1,点A在x轴的正半轴上,B为⊙O上一点,过点A、B的直线与y轴交于点C,且OA2=ABAC.

(1)求证:直线AB是⊙O的切线;
(2)若AB=![]() ,求直线AB对应的函数表达式.
,求直线AB对应的函数表达式.
【答案】(1)见解析;(2)![]()
【解析】
,
(1)连接OB,根据题意可证明△OAB∽△CAO,继而可推出OB⊥AB,根据切线定理即可求证结论;
(2)根据勾股定理可求得OA=2及A点坐标,根据相似三角形的性质可得![]() ,进而可求CO的长及C点坐标,利用待定系数法,设直线AB对应的函数表达式为y=kx+b,再把点A、C的坐标代入求得k、b的值即可.
,进而可求CO的长及C点坐标,利用待定系数法,设直线AB对应的函数表达式为y=kx+b,再把点A、C的坐标代入求得k、b的值即可.
(1)证明:连接OB.
∵OA2=ABAC
∴![]() ,
,
又∵∠OAB=∠CAO,
∴△OAB∽△CAO,
∴∠ABO=∠AOC,
又∵∠AOC=90°,
∴∠ABO=90°,
∴AB⊥OB;
∴直线AB是⊙O的切线;
(2)解:∵∠ABO=90°,![]() ,OB=1,
,OB=1,
∴![]() ,
,
∴点A坐标为(2,0),
∵△OAB∽△CAO,
∴![]() ,
,
即![]() ,
,
∴![]() ,
,
∴点C坐标为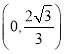 ;
;
设直线AB对应的函数表达式为y=kx+b,
则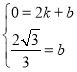 ,
,
∴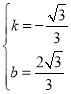
∴![]() .
.
即直线AB对应的函数表达式为![]() .
.


 天天向上口算本系列答案
天天向上口算本系列答案科目:初中数学 来源: 题型:
【题目】已知二次函数y=a![]() 4x+c的图象过点(1,0)和点(2,9),
4x+c的图象过点(1,0)和点(2,9),
(1)求该二次函数的解析式并写出其对称轴;
(2)当x满足什么条件时,函数值大于0?(不写求解过程),
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=x2﹣2x﹣1.
x | … | ﹣1 | 0 | 1 | 2 | 3 | … |
y | … |
|
|
|
|
| … |
(1)请在表内的空格中填入适当的数;
(2)根据列表,请在所给的平面直角坐标系中画出y=x2﹣2x﹣1的图象;
(3)当x在什么范围内时,y随x增大而减小;

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】关于二次函数y=x2+2x+3的图象有以下说法:其中正确的个数是( )
①它开口向下;②它的对称轴是过点(﹣1,3)且平行于y轴的直线;③它与x轴没有公共点;④它与y轴的交点坐标为(3,0).
A.1B.2C.3D.4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们约定,在平面直角坐标系中两条抛物线有且只有一个交点时,我们称这两条抛物线为“郡园牵手抛物线”,这个交点为“郡园点”.例如:抛物线![]() 与
与![]() 是“郡园牵手抛物线”,“郡园点”为
是“郡园牵手抛物线”,“郡园点”为![]() .
.
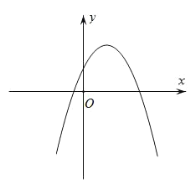
(1)如图,若抛物线![]() 与
与![]() 为“郡园牵手抛物线”,求
为“郡园牵手抛物线”,求![]() 的值;
的值;
(2)在(1)的条件下,若点![]() 是第一象限内抛物线
是第一象限内抛物线![]() 上的动点,过
上的动点,过![]() 作
作![]() 轴,
轴,![]() 为垂足,求
为垂足,求![]() 的最大值;
的最大值;
(3)在(1)的条件下,设点![]() 是抛物线
是抛物线![]() 与
与![]() 的“郡园点”,点
的“郡园点”,点![]() 是抛物线
是抛物线![]() 上一动点,问在抛物线
上一动点,问在抛物线![]() 的对称轴上是否存在点
的对称轴上是否存在点![]() ,使
,使![]() 是以点
是以点![]() 为直角顶点的等腰直角三角形?若存在,请直接写出点
为直角顶点的等腰直角三角形?若存在,请直接写出点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了减少雾霾的侵状,某市环保局与市委各部门协商,要求市民在春节期间禁止燃放烟花爆竹,为了征集市民对禁燃的意见,政府办公室进行了抽样调查,调查意见表设计为:“满意““一般””无所谓””反对”四个选项,调查结果汇总制成如下不完整的统计图,请根据提供的信息解答下面的问题.
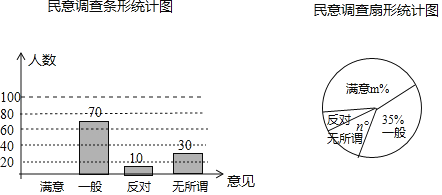
(1)参与问卷调查的人数为 .
(2)扇形统计图中的m= ,n= .补全条形统计图;
(3)若本市春节期间留守市区的市民有32000人,请你估计他们中持“反对”意见的人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
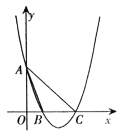
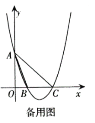
【题目】如图,抛物线![]() 交
交![]() 轴于
轴于![]() ,
,![]() 两点,交
两点,交![]() 轴于
轴于![]() 点,连接
点,连接![]() ,点
,点![]() 为抛物线上一动点.
为抛物线上一动点.
(1)求抛物线的解析式;
(2)当点![]() 到直线
到直线![]() 的距离为
的距离为![]() 时,求点
时,求点![]() 的横坐标;
的横坐标;
(3)当![]() 和
和![]() 的面积相等时,请直接写出点
的面积相等时,请直接写出点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
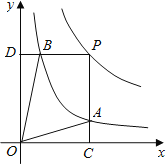
【题目】函数y=![]() 和y=
和y=![]() 在第一象限内的图象如图,点P是y=
在第一象限内的图象如图,点P是y=![]() 的图象上一动点,PC⊥x轴于点C,交y=
的图象上一动点,PC⊥x轴于点C,交y=![]() 的图象于点B.给出如下结论:①△ODB与△OCA的面积相等;②PA与PB始终相等;③四边形PAOB的面积大小不会发生变化;④CA=
的图象于点B.给出如下结论:①△ODB与△OCA的面积相等;②PA与PB始终相等;③四边形PAOB的面积大小不会发生变化;④CA=![]() AP.其中所有正确结论的序号是( )
AP.其中所有正确结论的序号是( )
A. ①②③ B. ②③④ C. ①③④ D. ①②④
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com