练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】已知二次函数y=a4x+c的图象过点(1，0)和点(2，9)，

    (1)求该二次函数的解析式并写出其对称轴；

    (2)当x满足什么条件时，函数值大于0？(不写求解过程)，

    【答案】（1），；（2）当x＜或x＞5时，函数值大于0．

    【解析】

    （1）把（-1，0）和点（2，-9）代入y=ax2-4x+c，得到一个二元一次方程组，求出方程组的解，即可得到该二次函数的解析式，然后求出对称轴；

    （2）求得抛物线与x轴的交点坐标后即可确定正确的答案．

    解：（1）∵二次函数的图象过点(1，0)和点(2，9)，

    ∴，

    解得：，

    ∴；

    ∴对称轴为：；

    （2）令，

    解得：，，

    如图：

    ∴点A的坐标为（，0），点B的坐标为（5，0）；

    ∴结合图象得到，当x＜或x＞5时，函数值大于0．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】在平面直角坐标系xOy中，一次函数y＝2x+b的图象与x轴的交点为A（2，0），与y轴的交点为B，直线AB与反比例函数y＝的图象交于点C（﹣1，m）．

    （1）求一次函数和反比例函数的表达式；

    （2）直接写出关于x的不等式2x+b＞的解集；

    （3）点P是这个反比例函数图象上的点，过点P作PM⊥x轴，垂足为点M，连接OP，BM，当S△ABM＝2S△OMP时，求点P的坐标．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在平面直角坐标系中，直线AB与x轴，y轴分别交于A，B，与反比例函数（k＞0）在第一象限的图象交于点E，F，过点E作EM⊥y轴于M，过点F作FN⊥x轴于N，直线EM与FN交于点C，若，则△OEF与△CEF的面积之比是（　　）

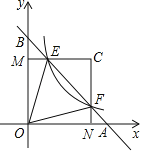
    A.2：1B.3：1C.2：3D.3：2

    查看答案和解析>>

    科目：初中数学 来源： 题型：

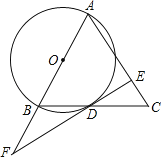
    【题目】如图，在△ABC中，AB＝AC，以AB为直径作⊙O交BC于点D，过点D作⊙O的切线DE交AC于点E，交AB延长线于点F．

    （1）求证：DE⊥AC；

    （2）若AB＝10，BF＝，求AE的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】 为满足社区居民健身的需要，市政府准备采购若干套健身器材免费提供给社区，经考察，劲松公司有两种型号的健身器可供选择.

    （1）劲松公司2015年每套型健身器的售价为万元，经过连续两年降价，2017年每套售价为 万元，求每套型健身器年平均下降率 ；

    （2）2017年市政府经过招标，决定年内采购并安装劲松公司两种型号的健身器材共套，采购专项费总计不超过万元，采购合同规定：每套型健身器售价为万元，每套型健身器售价我 万元.

    ①型健身器最多可购买多少套？

    ②安装完成后，若每套型和型健身器一年的养护费分别是购买价的 和 .市政府计划支出 万元进行养护.问该计划支出能否满足一年的养护需要？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】在平面直角坐标系中，二次函数y=x2+2x﹣3的图象如图所示，点A（x1，y1），B（x2，y2）是该二次函数图象上的两点，其中﹣3≤x1＜x2≤0，则下列结论正确的是（　　）

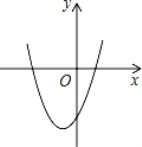
    A. y1＜y2B．y1＞y2C．y的最小值是﹣3 D．y的最小值是﹣4

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】下面是小元设计的“作已知角的角平分线”的尺规作图过程．

    已知：如图，∠AOB．

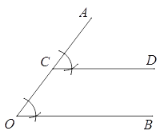
    求作：∠AOB的角平分线OP．

    作法：如图，

    ①在射线OA上任取点C；

    ②作∠ACD=∠AOB；

    ③以点C为圆心CO长为半径画圆，交射线CD于点P；

    ④作射线OP；

    所以射线OP即为所求．

    根据小元设计的尺规作图过程，完成以下任务．

    （1）补全图形；

    （2）完成下面的证明：

    证明：∵ ∠ACD=∠AOB，

    ∴ CD∥OB（____________）（填推理的依据）．

    ∴∠BOP=∠CPO．

    又∵ OC=CP，

    ∴∠COP=∠CPO（____________）（填推理的依据）．

    ∴∠COP=∠BOP．

    ∴ OP平分∠AOB．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】工人师傅用一块长为10dm，宽为6dm的矩形铁皮制作一个无盖的长方体容器，需要将四角各裁掉一个正方形．（厚度不计）

    （1）在图中画出裁剪示意图，用实线表示裁剪线，虚线表示折痕；并求长方体底面面积为12dm2时，裁掉的正方形边长多大？

    （2）若要求制作的长方体的底面长不大于底面宽的五倍，并将容器进行防锈处理，侧面每平方分米的费用为0.5元，底面每平方分米的费用为2元，裁掉的正方形边长多大时，总费用最低，最低为多少？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在平面直角坐标系中，⊙O的半径为1，点A在x轴的正半轴上，B为⊙O上一点，过点A、B的直线与y轴交于点C，且OA2＝ABAC．

    （1）求证：直线AB是⊙O的切线；

    （2）若AB＝，求直线AB对应的函数表达式．

    查看答案和解析>>

    同步练习册答案